Автокорреляция биржевых цен и рулетки в казино

Представляет интерес сравнить между собой функции автокорреляции выпадения чисел в рулетке в казино и поведения биржевых цен, по которым достаточно большие объемы торгов.

Данный интерес связан с тем, что порой встречается утверждение, что зарабатывание денег на бирже (а также на Форексе и на бинарных опционах), это аналог игры в рулетку. То есть, якобы, прогнозировать биржевые цены также невозможно, как и предсказать выпадение следующего числа в рулетке.

В качестве критерия предсказуемости временного ряда будем рассматривать функцию автокорреляции процесса. В реальной жизни мы имеем дело всегда не с бесконечными по времени функциями, а с конечной выборкой. Поэтому в качестве такой эмпирической функции автокорреляции будем рассматривать зависимость корреляции между временным рядом полной длины и его отрезком меньшей длины (скользящим окном) в зависимости от смещения скользящего окна. Скользящее окно всегда берется, начиная от первого элемента выборки.

В статье "Автокорреляция линейной функции с шумом" можно посмотреть, как ведет себя такая эмпирическая функция автокорреляции, когда линейный тренд начинает тонуть в чисто случайном непредсказуемом шуме. В статье "Автокорреляция синуса с шумом" можно посмотреть, как ведет себя эмпирическая функция автокорреляции, когда функция синус (прогнозируемый боковой тренд) начинает тонуть в чисто случайном непредсказуемом шуме.

Если мы имеем дело с непредсказуемым процессом, то следующее значение никак невозможно предсказать по предыдущим числам. Напомню, что теоретическая функция автокорреляции для такого бесконечного процесса будет R(0)=1 и R(t)=0 для t>0.

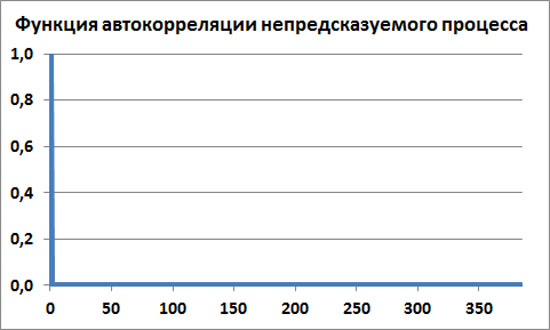
Смысл такой зависимости в том, что нет никаких статистических корреляций между любым начальным участком процесса и его продолжением. (Кроме точки t=0, которая соответствует тривиальному случаю, когда рассматривается корреляция между двумя тождественными процессами.)

А здесь мы сравним эмпирическую функцию автокорреляции чисел, выдаваемых европейской рулеткой, и эмпирическую функцию автокорреляции дневных цен закрытия валютной пары EUR/USD.

Европейская рулетка

Европейская рулетка разделена на 37 одинаковых секторов, которые пронумерованы от 0 (зеро) до 36. На каждое вращение рулетки (спин) выпадает какое-нибудь из этих 37 чисел.

Часто игроки опасаются, что рулетка в онлайн казино может быть нечестной и специально подкрученной так, чтобы уменьшить их выигрыш. Но такие опасения никогда не встречаются для игры в демо-режиме. В демо-режиме игроки не играют с настоящими деньгами. Они только знакомятся с тем, на какие кнопки нужно нажимать, чтобы сделать ту или иную ставку.

Поэтому возьмем результат 1000 последовательных спинов, записанных с демо-режима в одном из онлайн казино. Вот как эта выборка выглядит на графике.

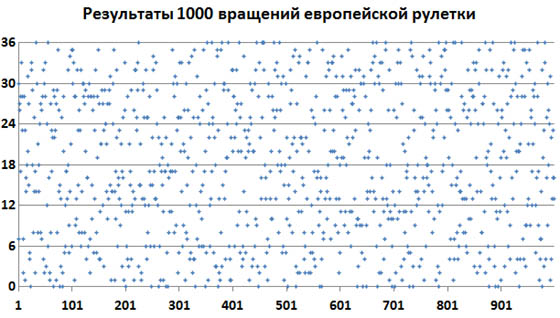
По горизонтали отложены номера последовательных спинов. По вертикали отложены номера выпавших чисел.

Посмотрим эмпирические функции автокорреляции этой выборки для скользящих окон размером 100, 250, 500, 750 и 900 первых спинов.

Скользящее окно 100 спинов

Для скользящего окна в 100 первых спинов при t=0 эмпирическая функция автокорреляции равна единице, как и должно быть. А затем её значение резко падает к среднему значению ноль. И там, возле нуля, эта функция совершает хаотические колебания.

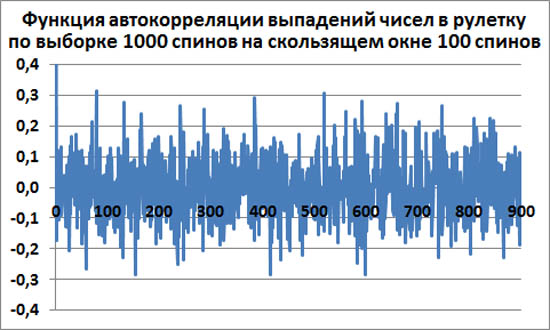
Среднеквадратичное отклонение функции автокорреляции от нуля для t>0 равно примерно σ=0.0997.

Скользящее окно 250 спинов

Для скользящего окна в 250 первых спинов при t=0 эмпирическая функция автокорреляции равна единице. Потом она резко уменьшается к среднему значению ноль. Затем, возле нуля, эта функция совершает хаотические колебания.

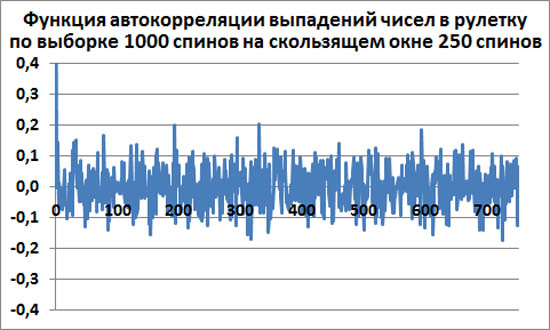
Среднеквадратичное отклонение функции автокорреляции от нуля для t>0 равно примерно σ=0.0631.

Скользящее окно 500 спинов

Для скользящего окна размером 500 первых спинов при t=0 эмпирическая функция автокорреляции равна единице. Далее она падает к среднему значению ноль. И возле нуля, она совершает хаотические колебания.

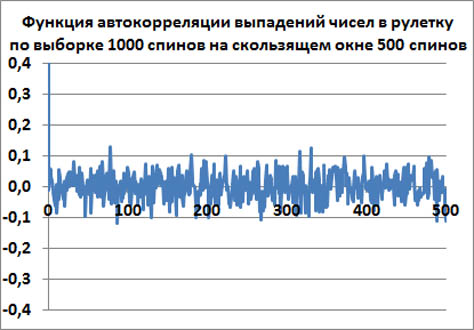
Среднеквадратичное отклонение функции автокорреляции от нуля для t>0 равно примерно σ=0.0452.

Скользящее окно 750 спинов

Для скользящего окна размером 750 спинов при t>0 эмпирическая функция автокорреляции падает от единицы до нуля и далее хаотически движется около нуля.

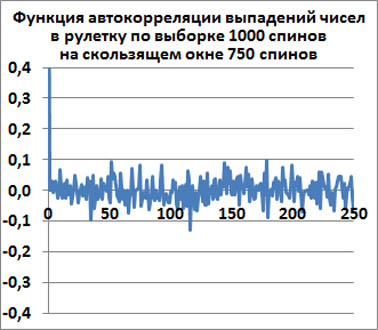
Среднеквадратичное отклонение функции автокорреляции от нуля для t>0 равно примерно σ=0.0366.

Скользящее окно 900 спинов

Для скользящего окна 900 спинов при t>0 эмпирическая функция автокорреляции падает от 1 до 0 и далее хаотически болтается около нуля.

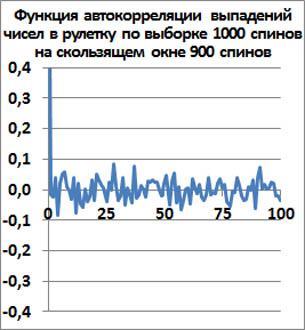
Среднеквадратичное отклонение функции автокорреляции от нуля для t>0 равно примерно σ=0.0333.

Среднеквадратичное отклонение

На следующем графике показано, что среднеквадратичное отклонение от нуля функции автокорреляции уменьшается с ростом размера скользящего окна.

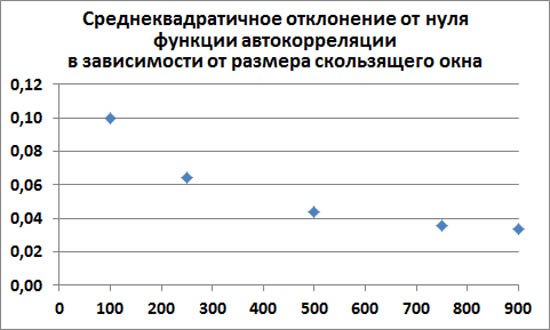
Хорошо видно, что среднеквадратичное отклонение убывает примерно также, как оно убывало для линейного тренда, утопленного в очень сильном случайном непредсказуемом шуме, созданном генератором случайных чисел. (См. статью по ссылке выше.) Среднеквадратичное отклонение здесь стремится тоже примерно к 0.03. И это не случайно. Ведь здесь выборка тоже взята из 1000 значений.

Также можно обнаружить, что предел, к которому стремиться среднеквадратичное отклонение при увеличении размера окна, убывает при увеличении размера выборки.

Таким образом, при стремлении числа спинов и размера скользящего окна к бесконечности, среднеквадратичное отклонение стремиться в ноль. А функция автокорреляции для выпадения чисел в рулетку переходит в теоретическую функцию автокорреляции: R(0)=1 и R(t)=0 для t>0.

Вывод для рулетки

Итак, выпадение чисел в рулетке принципиально непредсказуемо, ни по какому количеству результатов предыдущих спинов.

Процесс выпадения чисел в европейской рулетке с высокой степенью точности представляет собой белый шум с равнораспределением выпадающих целых чисел на интервале от 0 до 36, включительно.

Дневные цены закрытия валютной пары EUR/USD

Для сравнения с биржевыми ценами, возьмём тоже выборку из 1000 значений валютной пары EUR/USD. Конкретно, для исследования были взяты архивные данные дневных цен закрытия с 01.01.2013 по 20.06.2016 в дилинг-центре одного из брокеров Форекса.

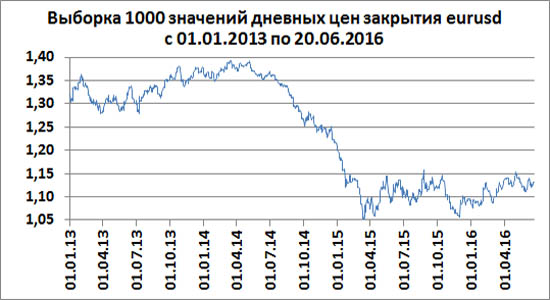
Рассмотрим те же самые размеры скользящих окон, как и для рулетки.

Скользящее окно 100 форекс-дней

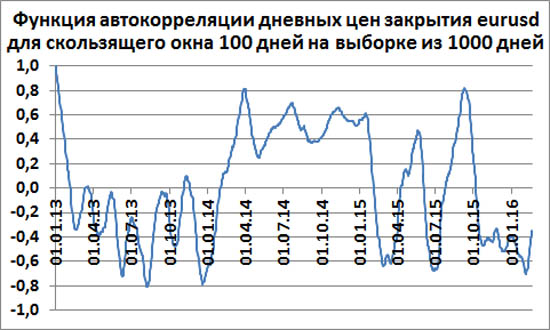
Сразу бросается в глаза, что функция автокорреляции не стремиться к нулю, а совершает сильные непериодические колебания. И не видно, чтобы амплитуда этих колебаний уменьшалась бы к нулю.

Эта Функция автокорреляции чем-то похожа на функцию автокорреляции синуса с небольшим шумом. Отличие состоит только в том, что отсутствует строгое значение периода и амплитуды колебаний.

Таким образом, некоторые участки дневного графика цен закрытия EUR/USD достаточно сильно коррелируют между собой, некоторые достаточно сильно антикоррелируют между собой, а некоторые совсем не коррелируют между собой. (Замечание для продвинутых в математике: Разумеется, речь идет только о линейной корреляции.)

Скользящее окно 250 форекс-дней

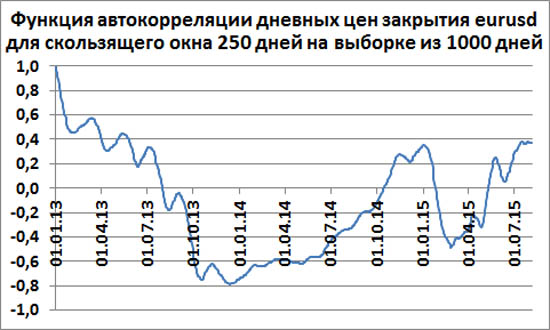
Для окна 250 форексных дней функция автокорреляции также не стремится к нулю, а совершает колебания достаточно большой амплитуды.

Увеличивается время полного "отшибания памяти" процесса (первое пересечение с нулем). Для скользящего окна 100 дней, "память" пропадала примерно через месяц. А для окна 250 дней "память" полностью пропала через 7 месяцев.

Скользящее окно 500 форекс-дней

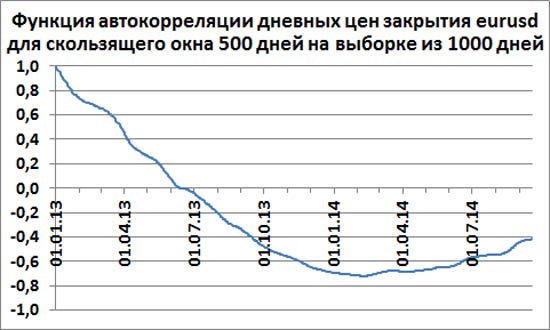
Для окна 500 форексных дней функция автокорреляции тоже не стремится к нулю, а уверенно проскакивает точку ноль и уходит в достаточно глубокую антикорреляцию до значения R=-0.71. Пересечение ноля происходит примерно через шесть с половиной месяцев.

Скользящее окно 750 форекс-дней

Интервал 750 дней уже достаточно большой для выборки 1000 дней. Поэтому функция автокорреляции уже не успевает пересечь точку ноль. Этот случай не слишком интересен.

Скользящее окно 900 форекс-дней

Случай для окна 900 дней совсем неинтересен, так как 900 очень близко к 1000. Понятно, что за интервал 1000-900=100 форексных дней (примерно 4 месяца) в большинстве точек ценового графика характер трендов не меняется. Случай окна 900 точек здесь показан просто для полноты картины.

Вывод для биржевых цен

Эмпирическая функция автокорреляции биржевых цен принципиально отличается от эмпирической функции автокорреляции выпадений чисел в рулетке.

Кроме того, эмпирическая функция автокорреляции биржевых цен ничуть не похожа на теоретическую функцию автокорреляции непредсказуемого процесса.

Основные статистические особенности поведения биржевых цен и их прогнозируемости:

• Функция автокорреляции биржевых цен не падает сразу в ноль. Значит, существует статистическая зависимость следующей цены от предыдущих цен на некотором интервале в прошлом. Этот интервал в прошлое примыкает к сегодняшнему моменту.
• Функция автокорреляции падает от R(0)=1 до значения R=0 монотонно (или с небольшими колебаниями). Значит, чем дальше от сегодняшнего дня в прошлом находится цена, тем меньше она влияет на завтрашнюю цену. И, наоборот, чем ближе к сегодняшнему дню в прошлом находится цена, тем больше она влияет на завтрашнюю цену.
• Функция автокорреляции совершает достаточно сильные колебания. Среднеквадратичное отклонение этих колебаний от нуля не стремится к нулю. Функция автокорреляции может высоко подняться в область сильной корреляции и сильно опуститься в область сильной антикорреляции. Значит, время от времени на ценовом графике появляются участки статистически похожие на участки, которые уже встречались в прошлом. Поэтому биржевые цены могут прогнозироваться с использованием паттернов.

Итак, биржевые цены обладают способностью к прогнозированию. Причем, их можно прогнозировать и по последовательной серии предыдущих цен, которые только что были, и по паттернам, которых уже давно не было на ценовом графике.

Но функция автокорреляции биржевых цен никогда не равна значению +1 (кроме t=0) и значению -1 для окон достаточно больших размеров. Это говорит о том, что прогнозируемость на все 100% принципиально невозможна. Прогнозируемость биржевых цен, принципиально, имеет вероятностный характер.

Любой метод прогнозирования биржевых цен всегда имеет следующие свойства:

• Часть прогнозов будут верными, а часть прогнозов будут неверными. Это соотношение количества верных и неверных прогнозов с течением времени по своему меняется у любого метода прогнозирования. Поэтому необходимо искать такие методы прогнозирования, которые на данный момент дают наибольшее количество верных прогнозов. И нужно не забывать, что найденный метод прогнозирования не всегда будет давать наибольшую долю верных прогнозов. То есть нужно вовремя менять свои методы прогнозирования.
• Чередование верных и неверных прогнозов, в общем случае, непредсказуемо. Но, в некоторых случаях, например, в тренде, более вероятна продолжительная серия верных прогнозов. Поэтому нужно стараться не входить в рынок (или входить меньшим капиталом) когда нет уверенности, что текущий метод прогнозирования выдает серию верных прогнозов.

Если кто-то ещё раз Вам скажет, что фондовая биржа, Форекс и бинарные опционы, это рулетка, то покажите ему эту статью.