Прогноз волн Эллиотта
Продолжаем тестирование нашей методики прогнозирования. Вы уже видели, как наш метод прогнозирования справляется с выявлением хороших синусоидальных закономерностей в сильных случайных шумах на примере Одиночного синусоидального тренда с шумом и Двух синусоидальных трендов с шумом. Теперь хотелось бы, во-первых, посмотреть что-то более реалистичное и близкое к поведению валют, а, во-вторых, посмотреть что-то не синусоидальное.
Мы это сейчас исследуем на примере волн Эллиотта. Волны Эллиотта тоже можно аппроксимировать какими-нибудь синусоидами. Но мы принципиально не будем делать такую модель. Просто, сейчас уже хочется опробовать метод на чем-то более сложном. Поэтому все волны Эллиотта будем аппроксимировать только прямыми линиями (кривыми первого порядка). Понятно, что если метод прогнозирования работает даже на таком материале, где идут изломы прямых и тем самым не существуют первые производные и все производные более высокого порядка, то значит, наш метод тем более будет работать на более гладких кривых более высокого порядка.
Исходные данные, для всех приведенных тут примеров брались из xls-файла для зашумленных волн Эллиотта. В колонке B дана сама модель волн Эллиотта, построенная из прямых линий с точечными изломами. В колонке C к этой функции из линейных отрезков с помощью генератора случайных чисел добавлен случайный белый шум с максимальной амплитудой равной единице. В колонках D, E и F находятся начальные данные с теми же самыми линейными волнами Эллиотта с добавлением белого шума амплитудами равными, соответственно, 2, 4 и 8 единиц. И напоминаем, что генератор случайных чисел в программе Excel пересчитывает свои значения каждый раз, как только Вы сохраняете файл или производите какие-то изменения внутри файла. Поэтому не надо удивляться, что в наших примерах случайный шум в точности не совпадает с тем, что Вы видите в скачанном файле исходных данных. Как было уже сказано в предыдущих примерах, конкретная реализация шума не влияет на качественный результат, если статистические характеристики шума (спектр, функция автокорреляции, среднее значение и дисперсия) остаются без изменений.
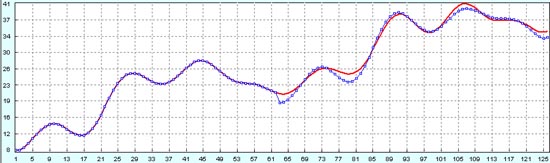
А это четыре графика, которые показывают зашумленные волны Эллиотта вместе с линейной моделью самих волн Эллиотта.
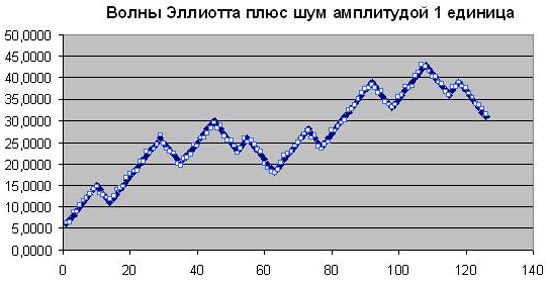
Итак, мы видим две крупные восходящие волны Эллиотта с их откатами. Это волны с номерами 1-4. Каждая из восходящих волн Эллиотта, в свою очередь, состоит из пяти волн Эллиотта более низкого порядка. А каждый откат, в свою очередь состоит из трех волн Эллиотта более низкого порядка. Обратите внимание, что при моделировании волн Эллиотта прямыми линиями, мы не учитывали слишком строго соотношения Фибоначчи. С одной стороны, это связано с тем, что нас волнует только качественный результат и принципиально ничего не должно меняться от соотношения длин волн. А, с другой стороны, это связано с тем, что мы сами не являемся слишком большими поклонниками чисел Фибоначчи. Мы считаем, что числа Фибоначчи в техническом анализе это скорее современная разновидность пифагорейства. Но мы не отрицаем тот психологический аспект, который могут иметь соотношения Фибоначчи на волнах Эллиотта, если все трейдеры по всему миру уверуют в эти соотношения и начнут закрывать свои позиции в строгом соответствии с этими соотношениями. Тогда действительно соотношения Фибоначчи будут работать на волнах Эллиотта на все 100%.
Задача заключается в том, чтобы посмотреть, как работает наш метод прогнозирования, получится ли спрогнозировать пятую крупную волну Эллиотта, состоящую из пяти более мелких волн. У нас заданы волны Эллиотта на 126 точках, и мы хотим посмотреть, что будет на следующих 50 точках. Если наш метод работает хорошо, то, по идее, на следующих 45 точках мы должны увидеть пятую большую волну Эллиотта, с 45-й по 50-ю точку мы должны обнаружить начало большого отката. И мы, конечно, хотим посмотреть, будет ли на этих следующих 45 точках спрогнозирована более мелкая структуру из первой волны до 136-й точки, вторая до 141-й точки и т.д.
Схема нашего исследования здесь точно такая же, как и в случае синусов. Мы сначала находим все тренды оригинального процесса и по первым главным трендам строим восстановленный процесс. Затем нам надо проверить, на сколько наш метод прогнозирования устойчив. Для этого мы берем данные восстановленного процесса на первых 63 точках и делаем прогноз на следующие 63 точки. (63+63=126.) Мы сравниваем этот прогноз с нашим восстановленным процессом, чтобы убедиться, что различие получается небольшое. Затем мы смотрим на то, как этот прогноз отличается от оригинального процесса. И, наконец, строим прогноз на будущие 50 точек с верхней и нижней границами доверительного интервала.
А начнем мы наше тестирование со случая нулевого шума. Для синусов случай нулевого шума не так интересен, так как синус это очень хорошая бесконечно дифференцируемая функция. А в случае волн Эллиотта представляет интерес посмотреть, как влияют на прогноз неаналитические точки в нашей модели.
Волны Эллиотта, моделируемые линейными функциями
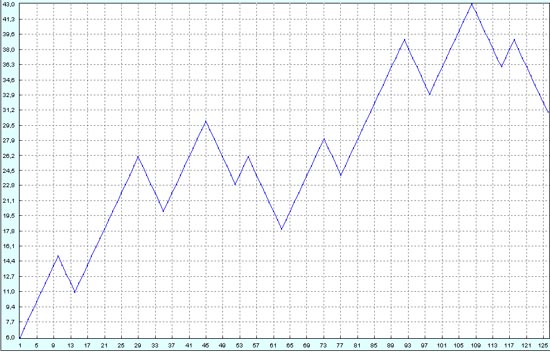
В отличие от синуса и других гладких аналитических функций, здесь полного совпадения восстановленной функции и оригинальной не будет никогда. Случай синуса без шума мы в предыдущих тестах не рассматривали, так как там уже первые одна-две компоненты полностью восстанавливали наши синусы. Аналогичный результат получается и при восстановлении других хороших функций, например, непрерывных полиномов. Поэтому нам эти примеры были неинтересны. Маленькие несовпадения восстановленного процесса и оригинального процесса там связано только с дискретностью данных. Получалось, что чем больше точек исходных данных, тем меньше была интегральная ошибка восстановленной функции. Итак, если функция на интервале аналитическая (то есть разлагается в хорошо сходящийся ряд в любой точке интервала), то можно сделать её аналитическое продолжение за пределы этого интервала в соответствии с теоремой аналитического продолжения.
А в случае, когда на интервале есть несколько неаналитических точек, так просто уже не получается сделать хорошее восстановление по одной-двум компонентам. Эта ситуация примерно такая же, как в случае обычного Фурье-разложения. В обычном Фурье-разложении чем функция более "синусоидальная", тем меньше нужно взять первых членов ряда Фурье, чтобы восстановить функцию с наперед заданной точностью. И чем более функция изломана или отличается от синусоиды, тем больше надо взять членов ряда Фурье, чтобы восстановить функцию с заданной точностью. В нашем методе всё точно также, только в качестве синуса может выступать любая аналитическая функция.
В нашем случае мы для восстановления берем столько первых трендовых компонент, чтобы восстановились все откаты. На рисунке ниже хорошо видно, что, например, на большом откате вторая маленькая волна на восстановленном процессе это именно откат вверх. То есть восстанавливаем процесс до тех пор, пока направление движения восстановленного процесса не будет повторять оригинальный процесс "по факту". Иначе говоря, где оригинал идет вверх, там и восстановленный процесс хотя бы частично тоже идет вверх, а где оригинал идет вниз, там и восстановленный процесс хотя бы на части участка идет тоже вниз.
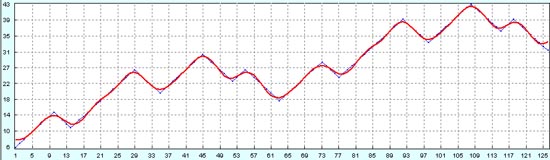
Как обычно берем половину нашего интервала, на котором заданы начальные данные, то есть первые 63 точки и по первым 63-м точкам восстановленного процесса пытаемся восстановить процесс на следующих 63 точках исторических данных. Как видно из рисунка ниже, мы имеем очень хороший результат, который показывает очень большую устойчивость метода прогнозирования.
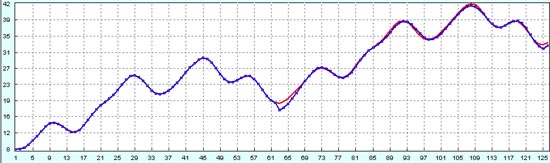
Здесь спрогнозированный таким способом процесс наложен на первоначальный оригинальный процесс для их сравнения.
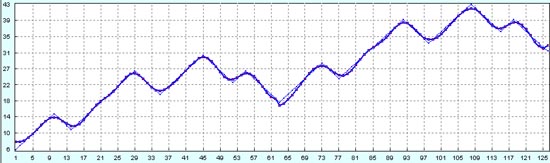
И вот, наконец, прогноз процесса в будущее на следующие 50 точек. Результат прогноза очень хороший. Периоды определены очень точно. Все максимумы и минимумы происходят точно там, где они и должны произойти. Только вот амплитуда колебаний волн Эллиотта получилась немного завышенной. При работе на откатах это не совсем хорошо.
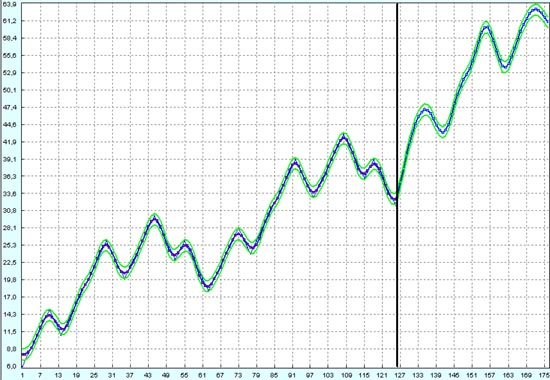
Как обычно, двумя зелеными линиями показаны границы доверительных интервалов 95%. Ширина доверительного интервала на прогнозе (справа от вертикальной черной линии) постоянно возрастает по мере движения в будущее. Но тем не менее, ширина этого интервала такая маленькая, что трейдеру можно работать на всех восходящих и на всех нисходящих волнах Эллиотта.
Ну, а далее посмотрим, как будут меняться наши прогнозы волн Эллиотта в будущее, если начать эти волны топить в случайном шуме.
Волны Эллиотта с шумом амплитудой 1
В таком маленьком шуме волны Эллиотта достаточно хорошо видны на глаз.
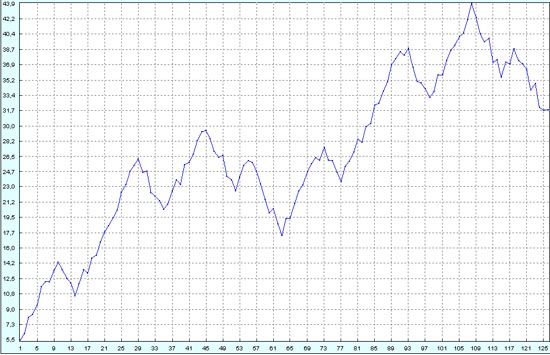
Делаем восстановление по имеющимся данным. Теперь не все откаты получаются ярко выраженными.
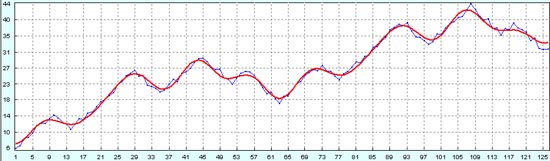
Смотрим, что получается для прогноза по первым 63-м точкам на следующие 63 точки исторических данных. Всё устойчиво.
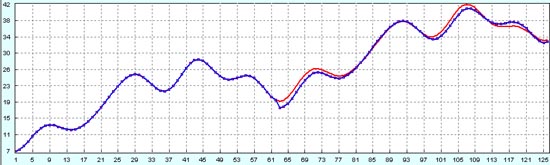
Далее, Вы можете увидеть сравнение оригинального процесса с восстановленным на первых 63 точках и с прогнозом на следующих 63 точках
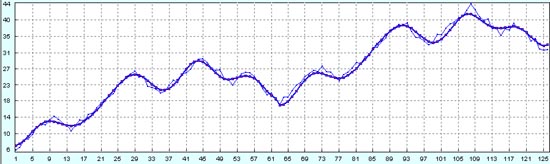
И вот прогноз на будущие 50 точек. Опять периоды определены очень точно, но амплитуды колебаний также немного завышены.
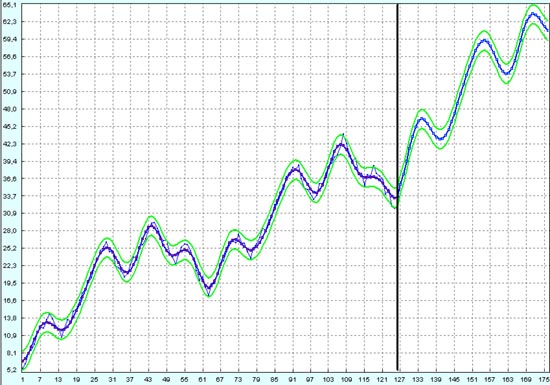
Доверительный интервал, ограниченный зелеными линиями, уже стал более широким. Он также уширяется при смещении вправо. Но он всё еще достаточно узкий, чтобы можно было иметь гарантированную прибыль даже на откатах.
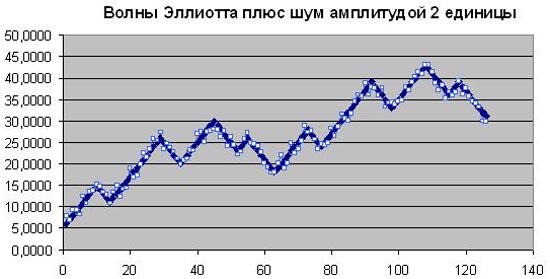
Волны Эллиотта с шумом амплитудой 2
В шуме с амплитудой 2 волны Эллиотта всё еще хорошо просматриваются.
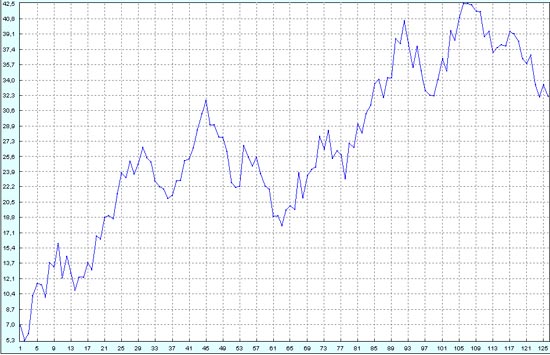
На восстановленном процессе уже проявились не все откаты.
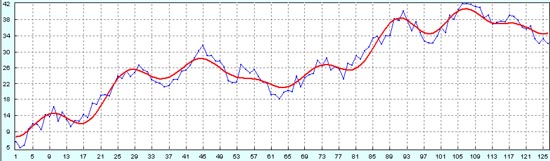
На исторических данных восстановление процесса идет нормально.
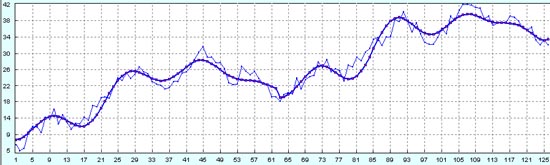
Сравниваем оригинальный процесс с восстановленными данными на первых 63 точках и сделанным по ним прогнозу на следующие 63 точки.
А вот и прогноз на будущие 50 точек. И снова очень хорошо спрогнозированы периоды, амплитуды колебаний уже не так завышены. как в случае шума амплитудой 1 и амплитудой 0. Прогноз первых 4 волн очень даже неплохой. Но вот пятая волна слишком короткая, а отката после нее вообще нет.
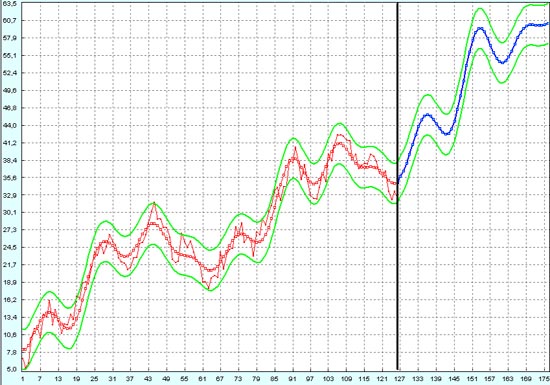
Доверительный интервал здесь уже на столько широкий, что получать гарантированную прибыль на откатах уже не получится. При таких широких доверительных интервалах прибыль на откатах можно не заработать, а только выиграть, то есть получить только случайно.
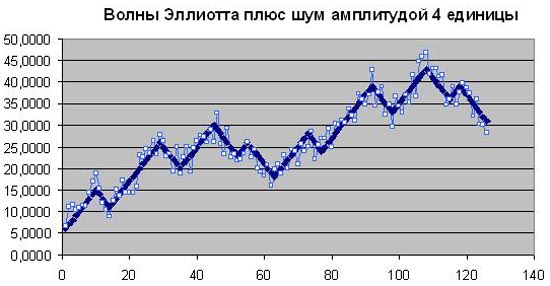
Волны Эллиотта с шумом амплитудой 4
Увеличиваем уровень случайного шума в 2 раза. Теперь чисто зрительно мы уже не видим маленьких волн Эллиотта, которые образуют структуру больших волн Эллиотта. Достаточно уверенно просматриваются только крупные волны Эллиотта.
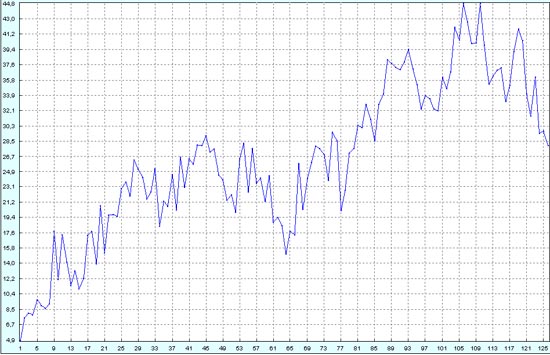
На восстановленном процессе эти мелкие волны Эллиотта тоже практически не распознаются. А шумовые колебания наводят мелкую "рябь" на восстановленный процесс.
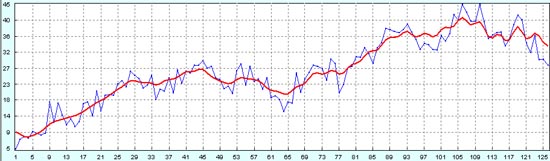
Эта мелкая "рябь" от шумов показывает больше отклонений восстановленного процесса от прогнозируемого процесса на исторических данных.
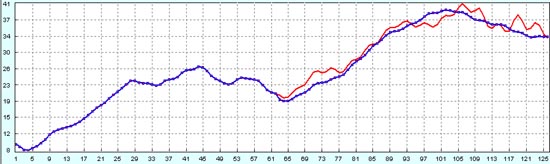
Далее, как обычно, оригинальный процесс и прогноз на исторических данных. Правая и левая части следующего графика качественно практически не отличаются друг от друга.
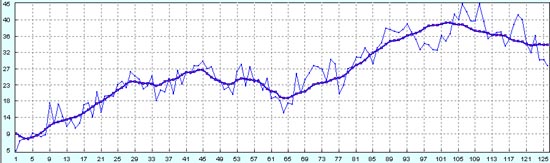
А на прогнозе на будущие точки мы уже не видим маленьких волн Эллиотта. Мелкая "рябь" на прогнозе появилась, видимо, оттого, что теперь наш метод прогнозирования схватывает какие-то случайные периоды, которые идут от случайного шума. Можно сказать, что удалось спрогнозировать пятую большую волну Эллиотта и начало отката за ней.
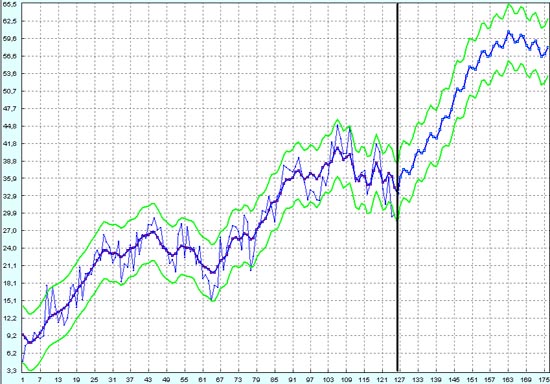
Гарантированную прибыль можно будет получить только на этой пятой волне Эллиотта. Доверительный интервал, ограниченный зелеными линиями, здесь достаточно широкий, чтобы уберечь нас от соблазна попытаться заработать на мелкой "ряби" нашего прогноза. И это правильно! Мы же знаем, что это ложные колебания, которые не связаны ни с какими трендами. Значит прогноз этой мелкой "ряби" неверный. Верный только прогноз пятой большой волны Эллиотта.
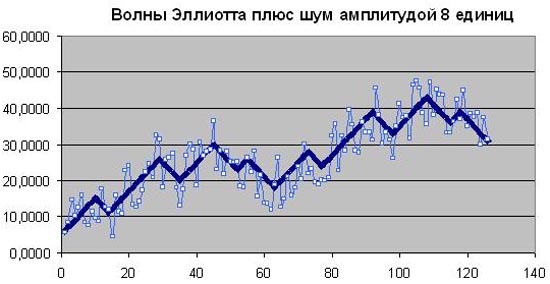
Волны Эллиотта с шумом амплитудой 8
Еще раз сделаем удвоение шума. Теперь даже сами большие волны Эллиотта угадываются с трудом.
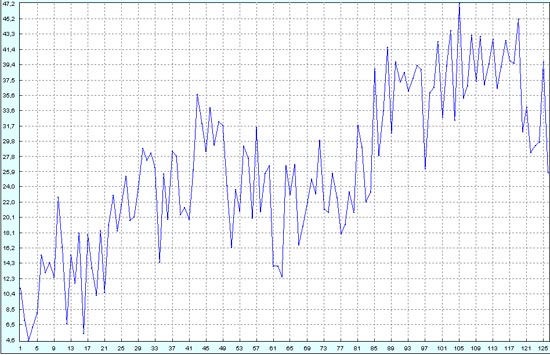
Нам приходится уменьшить число компонент для сборки восстановленного процесса. Иначе шумы наводят на восстановленном процессе случайную рябь достаточно большой амплитуды.
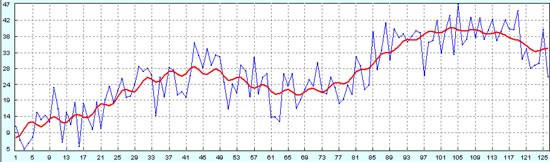
В этом причина того, что следующий график выглядит чуть более красивее, чем аналогичный для случая амплитуды шума равной 4.
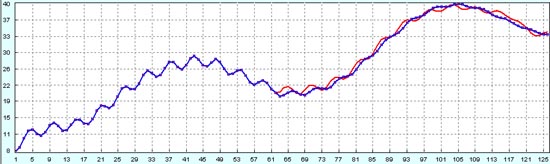
И следующий график тоже выглядит красивее.
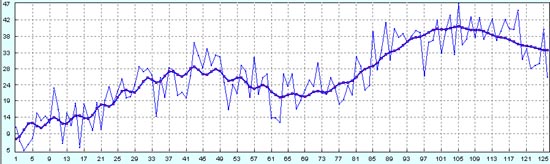
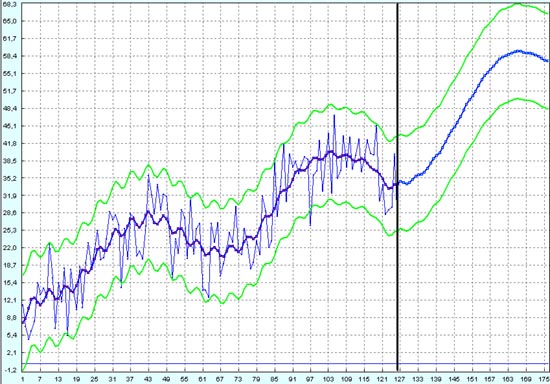
Прогноз на будущее хоть и дает нам уверенную пятую большую волну Эллиотта с началом отката по её завершении, но доверительный интервал уже на столько широкий, что гарантированная прибыль получается очень маленькой. Примерно от значения 42 до значения 49, то есть всего 7 единиц. Всё, что Вы на пятой волне Эллиотта заработаете свыше 7, будет Вами не заработано, а случайно выиграно.
...




