Прогноз двух зашумленных синусов
Продолжаем тестирование нашей методики прогнозирования. В отличие от теста зашумленного синуса, здесь рассмотрим тест двух периодических функций, с частотами, различающимися на порядок. Конкретно здесь частоты будут различаться в 10 раз. Возьмем два синуса и будем топить их в белом шуме, который сделаем при помощи генератора случайных чисел.
Всё рассмотрение будем проводить для уровней шумов:
- 50% шума от амплитуды синуса
- 100% шума от амплитуды синуса
- 200% шума от амплитуды синуса
Пусть оба синуса сначала имеют одинаковую амплитуду. Затем рассмотрим случай, когда они имеют разные амплитуды.
Пусть низкочастотный синус имеет период 10π, где π=3.14..., то есть примерно период 62,8 точек, а высокочастотный синус пусть имеет частоту в 10 раз большую, то есть период π, (около 6,28 точек). Начальные данные программе расчета прогноза давались по первым 101 точке.
Примеры, приведенные здесь, можно увидеть, скачав xls-файл для двух зашумленных синусов. Опять заметим, что генератор случайных чисел в Excell постоянно пересчитывает свои случайные числа при каждом сохранении файла. Поэтому наши данные начального графика здесь отличаются от тех, которые Вы видите в скачанном файле. Это сделано в Excel специально, чтобы генератор случайных чисел не начинался с одной и той же последовательности чисел. Как Вы понимаете, конкретная последовательность случайных чисел не играет никакой роли. Играют роль только характеристики этих случайных последовательностей, такие, как амплитуда, частотный спектр и функция автокорреляции.
А здесь приведены два графика зашумленных синусов, чтобы Вы наглядно увидели, как шум искажает два синусоидальных тренда, наложенных друг на друга.
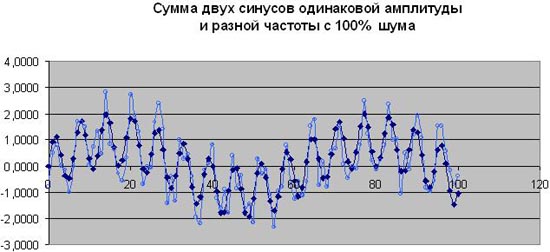
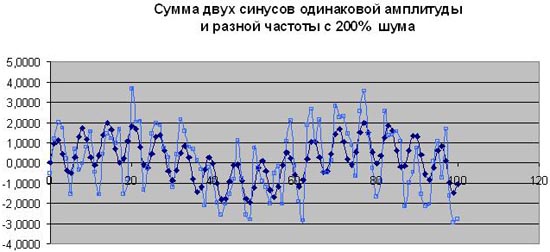
Мы опускаем исследование случая для шума 50% и двух одинаковых амплитуд синусоидальных процессов, так как там наша методика отлично справилась с заданием и дала очень хороший прогноз дальнейшего поведения процесса. Поэтому, для случая двух одинаковых амплитуд, посмотрим только на результаты компьютерного прогноза для шума амплитуды 100% и 200%. Понятно, что компьютер не знает ни о какой аналитике, так как нашей программе мы "скармливаем" только столбцы цифр.
Как и в случае одного синуса с шумом, далее все расчеты приведены для случая, когда для подбора оператора эволюции использовался подинтервал из 51 точки, то есть примерно половина от всего интервала из 101 точки на которой все данные процесса известны. В этот раз мы хотим посмотреть, как наш метод прогнозирует поведение двух главных трендов, низкочастотного и высокочастотного на следующих 50 точках с 102-ой точки до 151-ой точки.
Синусы одинаковой амплитуды с 100% шумом
Этот случай соответствует колонке D в скаченном Вами xls-файле примеров для двух синусов. В общем-то, высокочастотный синус практически утонул в шуме. Пока еще хоть как-то просматриваются глобальные тренды на колебаниях синуса низкой частоты. Но вот что на этот низкочастотный синус наложен еще один синус с шумом или наложен только один шум без синуса, это сказать на глазок уже невозможно.
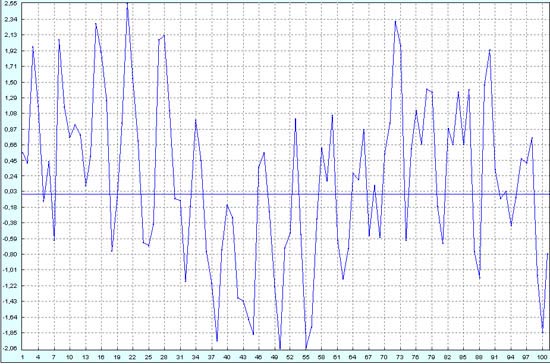
Но математика достаточно уверенно восстанавливает высокочастотные колебания очень похожие на синусоидальные (см. красную линию на графике ниже).
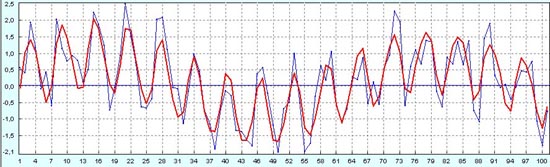
Давайте опять, как и в случае одного синуса, посмотрим прогноз по первым 50 точкам. На сколько будет отличаться прогноз процесса, сделанный только по первым 50 точкам, от восстановленного процесса на предыдущем графике с применением той же самой методики. На графике ниже хорошо видно, что метод довольно устойчивый. Мы спокойно могли бы делать прогноз не по 101 точке, а только по первым 50 точкам. Наш прогноз почти не отличается от восстановленного процесса. Расхождения на второй половине графика можно трактовать, как меру доверия к расчетам. Восстановленный график показан красной сплошной линией (как и на предыдущем графике), а прогноз по первым 50 точкам показан синим цветом. Разумеется, на первых 50 точках оба процесса совпадают, а во второй половине графика начинаются расхождения. Фактически это как бы проверка нашей методики на исторических данных, ведь данные на точках от 51-й до 101-й нам уже были известны. Из этой проверки на исторических данных мы и находим, на сколько можно доверять нашему методу прогнозирования.
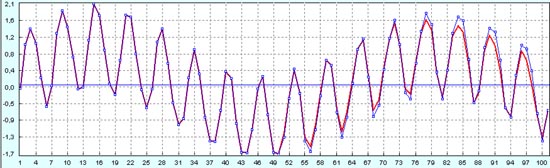
А здесь прогноз вторых 50 точек по первым 50 точкам из восстановленного тренда просто наложен на первоначальный график для сравнения, чтобы увидеть, как бы мы спрогнозировали вторую часть графика (толстая синяя линия, как на предыдущем графике) и какова была вторая часть графика в реальности первоначально (тонкая синяя линия).
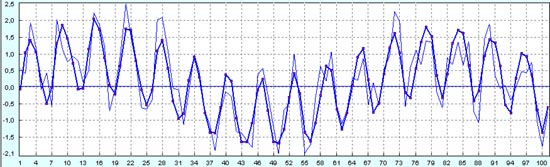
А вот и результат прогноза следующих 50 точек по первым 101 точкам. То есть это прогноз процесса в будущее, туда, где мы еще не видели, как процесс пойдет в реальности.
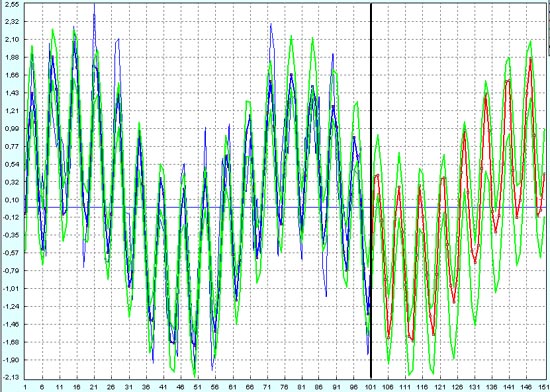
Зелеными линиями показаны верхняя и нижняя границы доверительных интервалов. Если бы это был реальный график курса валютной пары на рынке Форекс, то эти линии были бы ограничителями, внутри которых валютный курс меняется непредсказуемо. Работа трейдера между этими линиями может быть очень рискованной. Тут мы видим, что прогноз по высокочастотному тренду меняется на величину больше, чем ширина полосы между зелеными линиями. Поэтому при работе на высокочастотном тренде у трейдера будет гарантированная прибыль. А вот на низкочастотном тренде лучше не работать, так как самые низкие максимуму верхней зеленой линии лежат выше, чем самые высокие минимумы нижней зеленой линии.
Синусы одинаковой амплитуды с 200% шумом
Это данные из колонки E из нашего xls-файла. При наличии некоторой фантазии можно предположить, что тут имеются некоторые слабые низкочастотные тренды, но очень зашумленные.
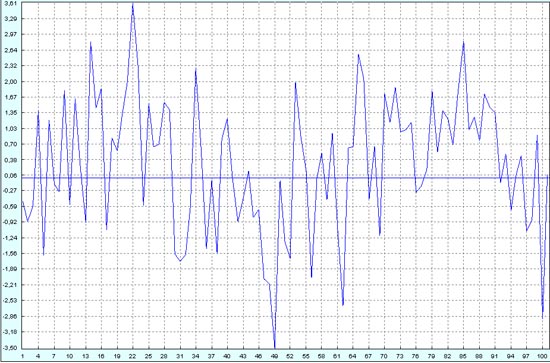
Тем не менее, наша математика уверенно восстанавливает из этого шума два синусоидальных процесса, наложенных друг на друга.
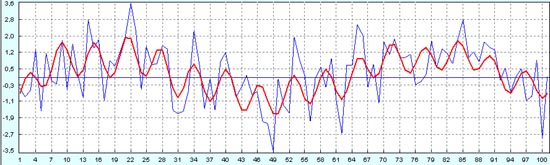
Далее опять показан график расхождений нашего восстановленного процесса с прогнозом, сделанным по первым 50 точкам с применением той же самой методики, по которой был найден восстановленный процесс. Поэтому на первых 50 точках у нас тут также полное совпадение с восстановленным процессом, а далее начинаются расхождения, которые показывают меру доверия к прогнозируемому методу. Восстановленный график показан красной сплошной линией, а прогноз по первым 50 точкам показан синим цветом. Здесь расхождения гораздо более значительные, чем те, что мы видели, когда уровень шума был только 100% от амплитуды.
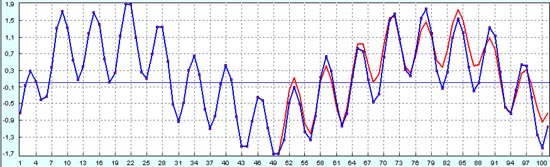
Если теперь сравнить прогноз вторых 50 точек по первым 50 точкам из восстановленного процесса с первоначальным процессом, то как будто бы между ними уже мало что общего. Во всяком случае, интуитивно никак нельзя из начального процесса (тонкая линия) нарисовать восстановленный процесс (толстая линия).
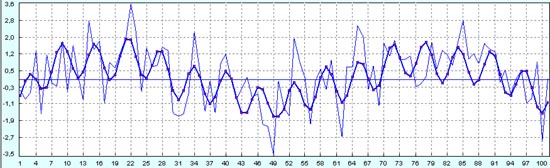
А вот и результат прогноза следующих 50 точек в будущее.
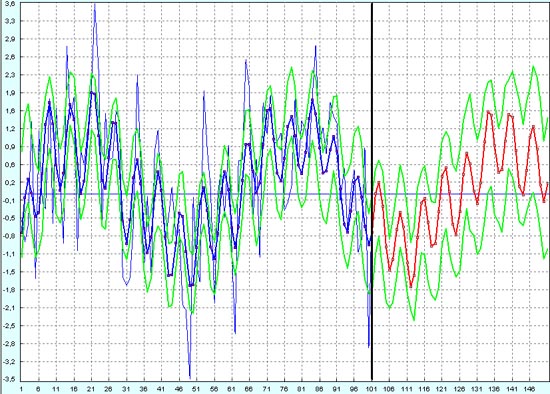
Зелеными линиями показаны верхняя и нижняя границы доверительных интервалов. Если бы это был реальный график курса валютной пары на бирже Форекс, то эти линии были бы ограничителями, внутри которых валютный курс меняется непредсказуемо. Здесь уже невозможно получить гарантированную прибыль и на высокочастотных колебаниях процесса. Единственное, что можно еще сделать, это если бы была куплена валюта на минимуме на 100-й точке, тогда гарантируется прибыль при закрытии позиции на какой-нибудь из следующих 50 точках. Но это у нас случайно так получилось, что именно на 100-й точке был очень сильный скачек вниз.
Высокочастотный синус с малой амплитудой и низкочастотный синус, и плюс 50% шума от низкочастотной амплитуды
Теперь посмотрим, что изменится, если синусы будут иметь разные амплитуды. Пусть сначала высокочастотный синусоидальный процесс имеет амплитуду в 2 раза меньше, чем низкочастотный процесс. Сильно большую разницу амплитуд не берем специально для наглядности. Нам главное сейчас проверить метод прогноза при разных условиях и посмотреть, что меняется в прогнозе.
Начнем наше исследование с уровня шума 50% от амплитуды низкочастотного процесса, так как уже при таком шуме высокочастотный процесс полностью тонет в шумах, что хорошо просматривается на графике ниже. Взята колонка G из xls-файла примеров.
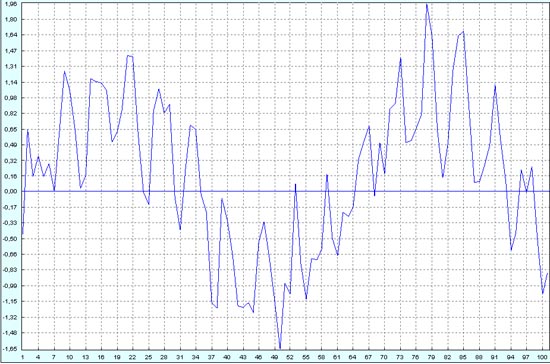
Как и ожидалось, математические методы очень уверенно распознают высокочастотный процесс.
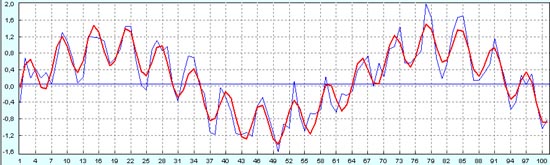
И вполне устойчиво распознают, что хорошо видно на сравнении восстановленного процесса и процесса спрогнозированного по первым 50 точкам. Восстановленный график показан красной сплошной линией, а прогноз по первым 50 точкам показан синим цветом.
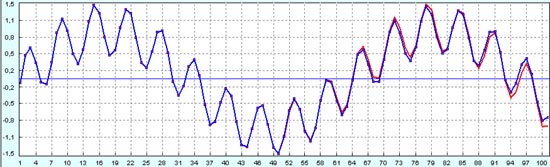
Прогноз вторых 50 точек по первым 50 точкам из восстановленного тренда здесь наложен на первоначальный график для сравнения.
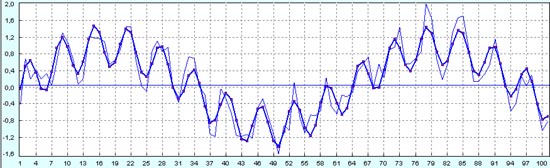
Наконец, прогноз будущих 50 точек для процесса, который является суммой высокочастотного синуса и низкочастотного синуса с шумом 50% от амплитуды низкочастотной компоненты.
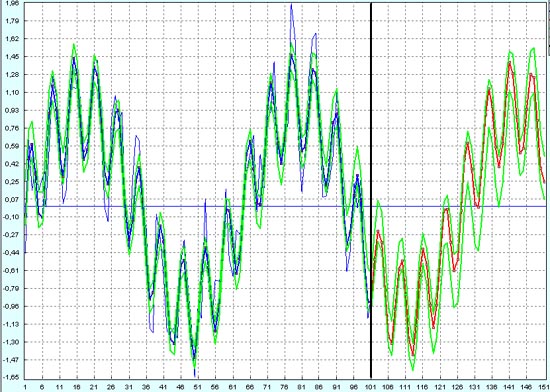
Здесь, как обычно, зелеными линиями показаны верхняя и нижняя границы доверительных интервалов. Если бы это был реальный график курса валютной пары на рынке Форекс, то эти линии были бы ограничителями, внутри которых валютный курс меняется непредсказуемо. Так как можно найти, где самые низкие максимумы верхней зеленой линии лежат ниже самых высоких минимумов нижней зеленой линии, то если бы это был бы случай реальной валютной биржи Forex, то здесь трейдер мог бы получить гарантированную прибыль и на высокочастотных колебаниях валюты и на низкочастотных.
Высокочастотный синус с малой амплитудой и низкочастотный синус, и плюс 100% шума от низкочастотной амплитуды
При шуме 100% о регулярных высокочастотных колебаниях догадаться уже совсем никак невозможно, так как уровень шума превышает их амплитуду в 2 раза. См. колонку H в xls-файле.
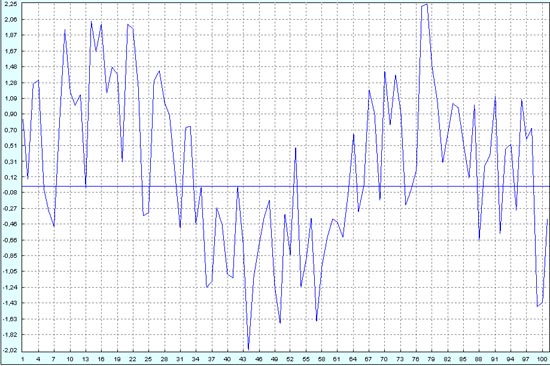
Тем не менее, наш вычислительный алгоритм снова оказался на высоте. Высокочастотная синусоида с половинной амплитудой просматривается на восстановленном процессе очень явно.
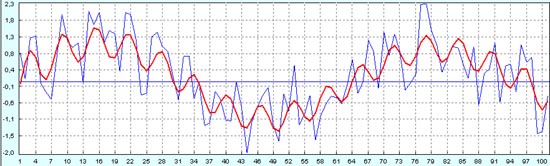
Далее, как обычно, делаем прогноз по первым 50 точкам, чтобы посмотреть расхождение с историческими данными.
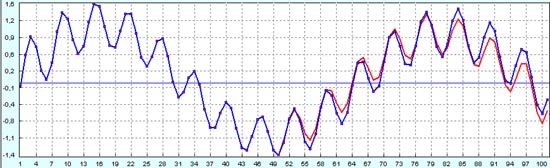
Сравниваем этот прогноз с реальной кривой.
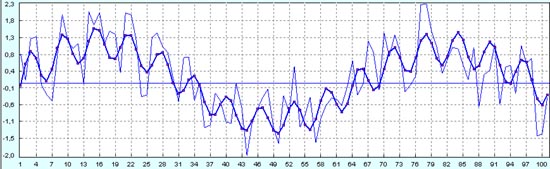
И делаем прогноз на будущие 50 точек после 101-й точки.
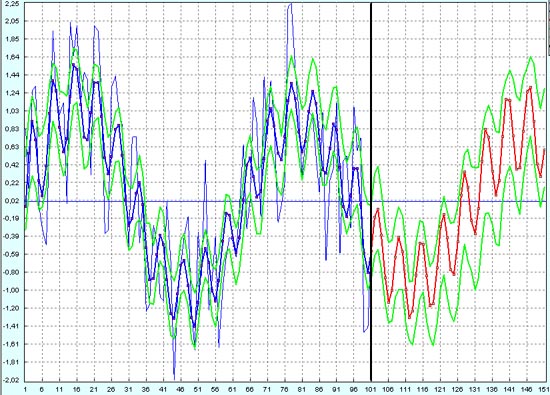
Вот здесь по высокочастотным колебаниям гарантированной прибыли уже не получим (за исключением пары небольших интервалов). Если бы это был реальный график поведения валютной пары, то здесь достаточно гарантировано получалась бы прибыль по низкочастотному тренду.
Высокочастотный синус с малой амплитудой и низкочастотный синус, и плюс 200% шума от низкочастотной амплитуды
При шуме 200% по высоким частотам идет уже полный хаос, так как амплитуда случайного шума превышает амплитуду регулярного высокочастотного процесса уже в 4 раза. (Колонка I из файла.) С некоторой натяжкой можно говорить, что здесь есть пара низкочастотных трендов. Но на самом деле это от лукавого. Просто мы знаем, что в этих шумах еще спрятан низкочастотный синус, вот и пытаемся найти его следы. А, встретив такой график в реальности на какой-нибудь валютной паре, мы скорее признаем, что тут мы имеем дело с горизонтальным трендом.
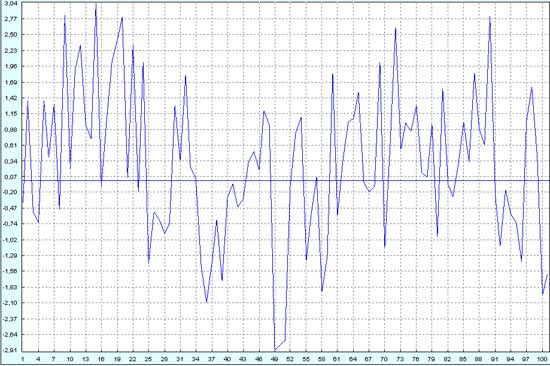
Математический метод здесь уже работает с некоторой натяжкой. Высокочастотная компонента еще как-то уверенно выявляется, а вот низкочастотная компонента нам кажется найденной только лишь потому, что мы знаем про нее заранее. Покажите этот график посторонним людям, и Вы увидите, что половина из них засомневается, есть ли тут еще один регулярный процесс с низкой частотой колебаний.
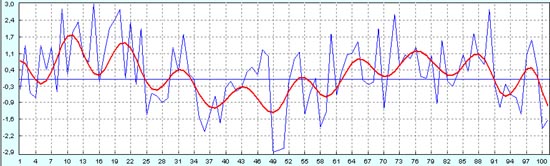
Сравнение прогноза по части данных с историческими данными демонстрирует хорошую устойчивость.
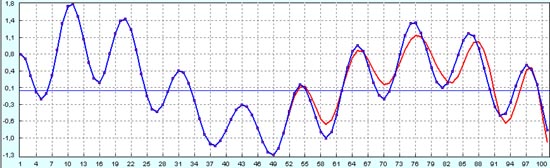
Обалденное впечатление от сравнения этого прогноза с тем, что реально было дано. Ну, как будто бы между ними ничего общего!
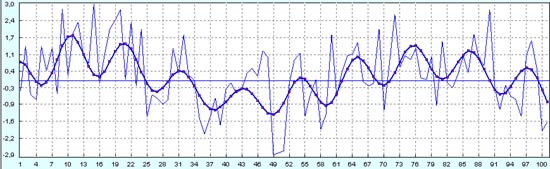
И вот что получаем в качестве прогноза на следующие 50 точек.
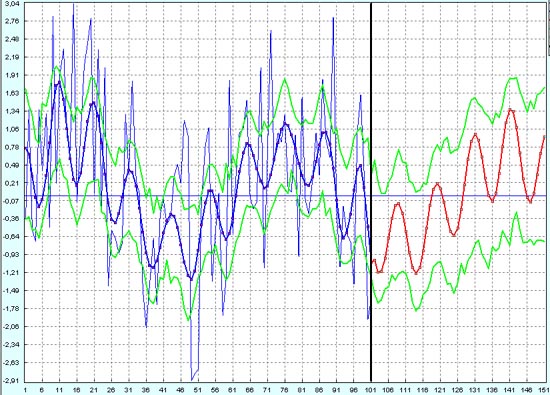
Как видите работать тут совершенно невозможно. Дилетанты здесь попытаются получить прибыль рассчитывая на чистое везения, а профессионалы уйдут с рынка.
Низкочастотный синус с малой амплитудой и высокочастотный синус, и плюс 50% шума от высокочастотной амплитуды
Осталось рассмотреть случай, когда, наоборот, высокочастотные колебания имеют амплитуду больше, чем низкочастотные колебания. Для Форекса это более редкая ситуация, поэтому рассмотрим её исключительно для полноты изложения и остановимся на ней очень кратко. Думаю, Вы сами всё поймете из приведенных тут графиков.
Рассматриваем снова разницу амплитуд в 2 раза, то есть низкочастотные колебания имеют амплитуду в два раза меньше высокочастотных, а уровень шума, как в предыдущем примере отсчитываем в процентах от амплитуды того процесса, который имеет большую амплитуду, в данном случае от амплитуды высокочастотного процесса. Начнем рассмотрение с шума 50%. (Колонка K из файла.)
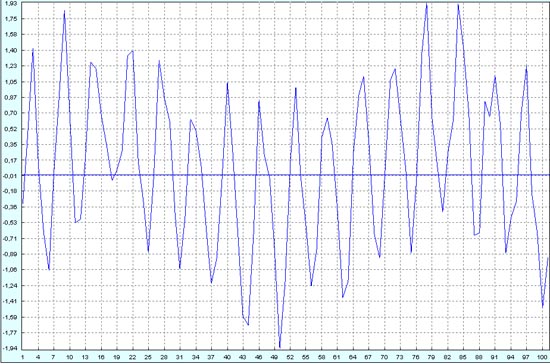
Высокочастотный синус отлично восстанавливается.
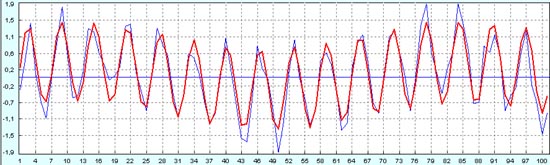
Отличная устойчивость метода.
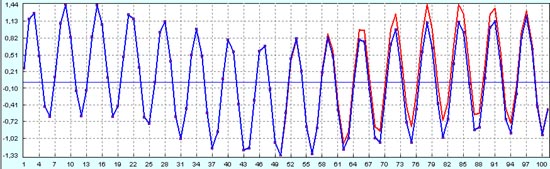
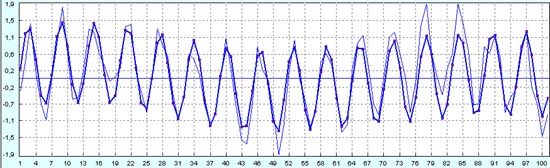
По начальным данным с хорошим глазомером можно было бы и так увидеть тут высокочастотный синус.
Вот и прогноз будущего развития процесса на следующие 50 точек.
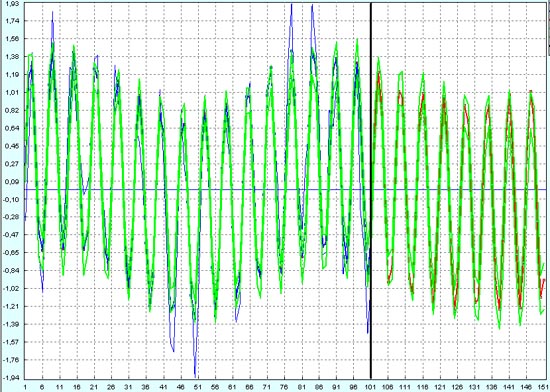
Понятно, что если бы это был реальный график на Форексе, то хорошую гарантированную прибыль можно было бы заработать на высокочастотных колебаниях валюты.
Низкочастотный синус с малой амплитудой и высокочастотный синус, и плюс 100% шума от высокочастотной амплитуды
Наращиваем шум до 100%. (Колонка L.)
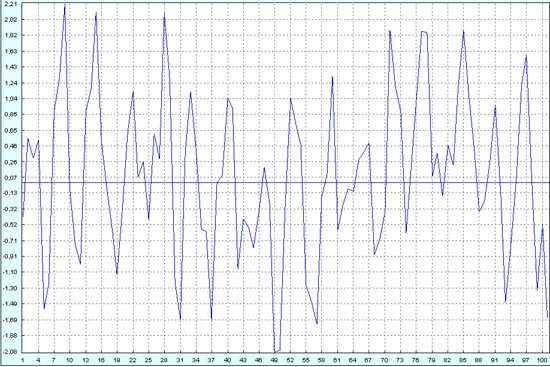
Но чего-то принципиально нового в качественном отношении не получаем.
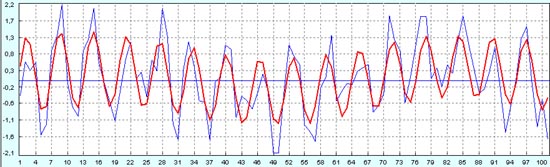
Качественно примерно то же самое, что и для 50% шума, только количественных расхождений больше при сравнении с историческими данными.
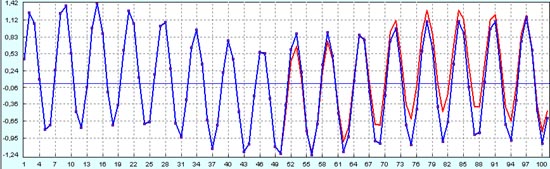
Ничего принципиально нового в качественном отношении невидно и при сравнении прогноза на исторических данных с реальным процессом.
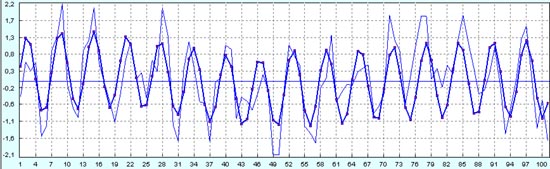
Прогноз на следующие 50 точек качественно ничего нового также не дает.
По-прежнему, гарантированную прибыть можно было бы заработать на высокочастотных колебаниях валюты.
Низкочастотный синус с малой амплитудой и высокочастотный синус, и плюс 200% шума от высокочастотной амплитуды
И, наконец, Наращиваем шум до 200% (колонка M).
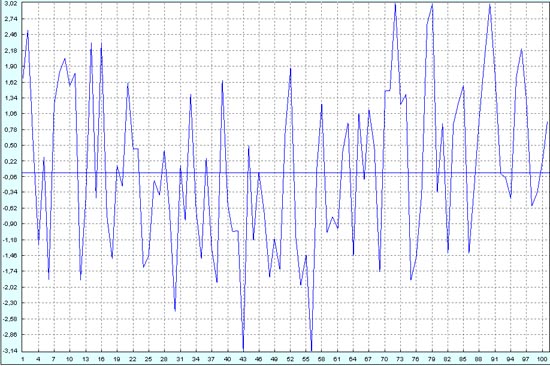
В математическом плане опять ничего принципиально нового не получаем.
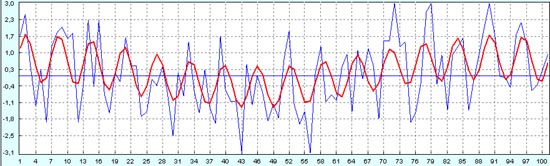
Естественно, что количественные расхождения при шуме 200% еще больше.
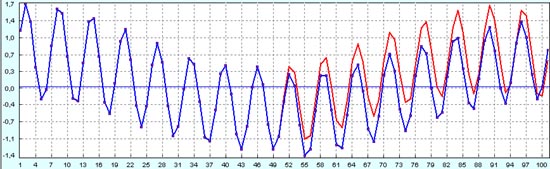
И количественное отличие прогноза на исторических данных от реальных данных еще больше.
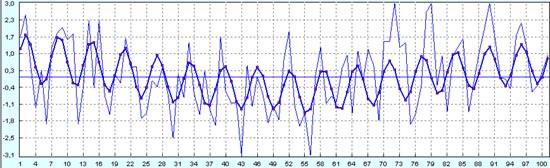
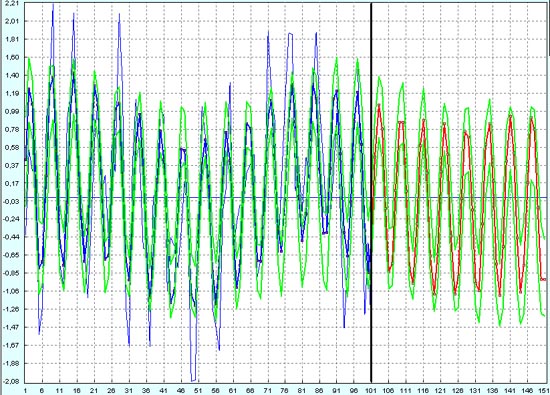
А вот прогноз на следующие 50 точек уже качественно совсем другой.
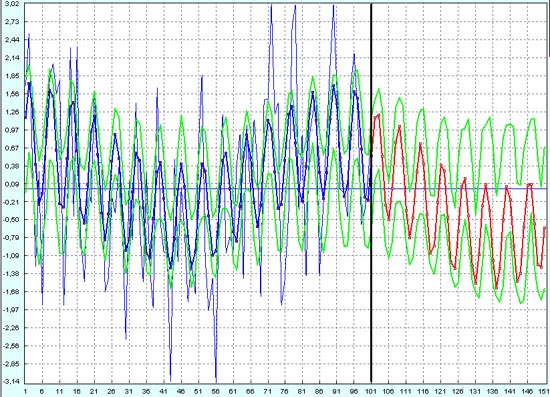
Здесь уже заработать гарантированную прибыль на высокочастотных колебаниях валюты не удается. Можно заработать только на случайном везении, так как стало слишком большим расстояние между минимумами верхней зеленой линии и максимумами нижней зеленой линией. При таких условиях лучше не входить в рынок и не открывать позиции.




