Виды процентных ставок

Пусть срок инвестирования будет равен одному или нескольким периодам владения активом. То есть, если период владения активом равен Т, то Т≥1. И пусть за один период владения активом проценты начисляются один или несколько раз. То есть, если за период начисляются проценты m раз, то m≥1.

Сначала рассмотрим случай, когда T=1 и m=1. То есть вложили деньги только на один период и в течение этого периода проценты начисляются только один раз.

Пусть P₀, это начальная сумма денег, которую вложили в финансовый актив, например в банковский депозит. Пусть J, это размер процентного дохода. И, наконец, P₁, это конечная сумма денег, которую получит инвестор.

Имеет смысл инвестировать, только если P₁>P₀. То есть J>0, так как P₁=P₀+J.

Существуют два способа вычисления процентов:

• Наращивание начальной суммы
• Скидка с конечной суммы

Процентные ставки с наращиванием начальной суммы

В этом случае процентная ставка (interest base rate) R вычисляется по очень простой формуле из математики для младших классов: J=RP₀. А так как P₁=P₀+J, то легко получаем, что
P₁ = P₀(1+R).

Это и есть основная формула, из которой находят простую (или декурсивную) процентную ставку R:

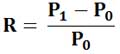
Обычным периодом владения T является один год. Если в году N дней, а срок владения инвестором финансового актива только n дней так, что n≤N, то вместо ставки R используется ставка R_n=nR/N. Тогда связь между начальными и конечными денежными суммами через процентную ставку R будет в виде:
P₁ = P₀(1+R_n) = P₀(1+nR/N), а J = P₀nR/N.

Процентные ставки со скидкой с конечной суммы

В этом случае считается, что конечная сумма, которую получит инвестор, уже известна. А нужно определить начальную сумму, которую надо вложить, чтобы в конце получилась такая конечная сумма.

Процентная ставка Q при таком учёте называется учётной ставкой, и её формула тоже очень простая: J=QP₁. Отсюда легко получить, что требуется начальная сумма:
P₀ = P₁(1-Q).

Если начальная и конечная суммы известны, то получаем формулу для простой учетной (или антсипативной) ставки Q:

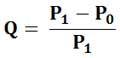
Так как стандартным периодом владения считается один год, а в году N дней, то если инвестор владеет финансовым активом всего n дней и n≤N, то вместо ставки Q используется ставка Q_n=nQ/N. Тогда связь между начальными и конечными денежными суммами через простую учетную ставку Q будет в виде:
P₀ = P₁(1-Q_n) = P₁(1-nQ/N), а J = P₁nQ/N.

Связь между двумя процентными ставками

Обе процентные ставки, декурсивная и антисипативная, являются характеристиками доходности инвестирования. Чем они больше, тем больше доходность. Чем больше декурсивная ставка R, тем больше будет конечная сумма при одной и той же начальной сумме. И чем больше антисипативная ставка Q, тем меньшего размера нужен начальный капитал, чтобы в конце получить одну и туже конечную сумму.

Если в предыдущих разделах используются одни и те же значения начального P₀ и конечного P₁ капитала, то обе процентные ставки связаны следующим соотношением:

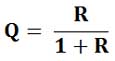
Отсюда видно, что всегда будет R>Q. Кроме того, легко показать, что

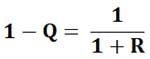
Отсюда можно еще получить, что (1-Q)(1+R)=1.

Из этих соотношений и из формулы для Q из предыдущего раздела получаем замечательную формулу:

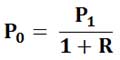
Получается, что начальная сумма равна дисконтированной стоимости (discounted value) конечной суммы. Поэтому учетную ставку Q называют ещё дисконтной ставкой (discount base rate) за период владения активом.

Множитель 1/(1+R) в последней формуле называется дисконтным множителем или, по другому, коэффициентом дисконтирования. А последнюю формулу ещё называют простой формулой дисконтирования.