Бесплатный онлайновый калькулятор волатильности
Смотрите очень полезный бесплатный онлайновый калькулятор волатильности.
Вы можете посчитать среднюю волатильность любой валютной пары (а также любого металла, фьючерса, акции или индекса) на любом тайм-фрейме за любой интервал времени. Усреднение ведется по выбранному интервалу. Интервал времени Вы устанавливаете сами (задаете в калькуляторе начальные и конечные дата и время).
Котировки для валютной пары берете в торговом терминале МетаТрейдер-4. Просто сохраняете их в текстовый файл и потом копируете любой нужный кусок данных в калькулятор. (Более подробную инструкцию см. на странице калькулятора).
Данный калькулятор волатильности считает среднюю амплитуду колебаний цены от цен закрытия для данного тайм-фрейма.
Знать волатильность очень полезно. Например, очень высока вероятность исполнения таких ордеров, которые расположены от уровня вхождения в рынок на расстоянии меньшим, чем волатильность. Такие ордера исполняются независимо от того, куда пойдет рыночный тренд. И тем более при горизонтальном тренде.
В то время, как если расположить ордер на расстоянии большем, чем волатильность, от точки вхождения в рынок, то вероятность исполнения такого ордера будет очень высокой только в том случае, если сформируется тренд в сторону этого ордера. И, наоборот, если тренд сформируется в противоположном направлении, то вероятность исполнения такого ордера очень низкая.
Например, если Вы расположили StopLoss в пределах волатильности, а TakeProfit за пределами волатильности, то более вероятно, что исполнится StopLoss, даже, если тренд пойдет в сторону ордера TakeProfit.
Если оба ордера, TakeProfit и StopLoss, Вы расположите в пределах волатильности, то результат будет непредсказуемый.
Если оба ордера, TakeProfit и StopLoss, Вы расположите за пределами волатильности, то исполнится тот ордер, в направлении которого пойдет тренд.
Таким образом, волатильность, это тот шум, который вносит элемент случайности в поведение биржевых цен.
Чем больше величина волатильности по сравнению с величиной тренда, тем хуже для трейдера.
Хорошие тренды, это такие тренды, которые меняют цену рыночного инструмента в десятки раз больше величины волатильности на данном тайм-фрейме. Очень трудно зарабатывать там, где величины трендов больше волатильности всего в 2-3 раза.
Обратите внимание, что волатильность на крупномасштабных тайм-фреймах превращается в тренды на мелких тайм-фреймах. Из-за этого факта можно в литературе и на форумах встретить следующую путаницу. Одни авторы утверждают, что чем больше волатильность, тем рискованнее данный рыночный инструмент. А другие авторы утверждают, что, наоборот, чем больше волатильность, тем больше возможностей заработка на колебаниях цен.
Теперь Вам понятно, что правы и первые авторы и вторые. Только вторые авторы рассматривают крупномасштабную волатильность на мелких масштабах времени, где крупномасштабная волатильность превращается в попеременно сменяющие друг друга тренды вверх и вниз.
На этих мелких тайм-фреймах с помощью калькулятора волатильности можно посчитать новое значение волатильности. Той самой волатильности, которая вносит риски в зарабатывании денег на колебаниях курса.
Полезные ссылки этого сайта:
- Рейтинг брокеров Форекс
- Как начать работать на Форексе без стартового капитала
- Торговые роботы
- Калькулятор волатильности
- Калькулятор ПАММ-трейдера
- Тест регулярных прогнозов рынка Форекс
- Какие валютные пары сейчас активно покупают трейдеры, а какие валютные пары они сейчас активно распродают
- Калькулятор расчета минимально необходимого количества прибыльных сделок по известному размеру плеча, доли капитала на каждую сделку, и необходимых отстроек ордеров TakeProfit и StopLoss от уровня вхождения в рынок
- Калькулятор расчета оптимальных уровней TakeProfit и StopLoss по их заданному соотношению, по известному размеру плеча, доли капитала на сделку и средней доле прибыльных сделок
------------------
Автор статьи: Евгений Миронов,
автор книг "Формула Келли для Форекса", "Продвинутый Мартингейл", "Математическое ожидание бинарных опционов", и др
Создатель Онлайнового калькулятора на базе нейросети "Прогнозирующая Машина" для прогноза будущих цен,
Создатель Онлайнового калькулятора для анализа и формирования диверсифицированного инвестиционного портфеля из активов мосбиржи.
Хомячковый рай. Уйти и потеряться:
Два критерия оценки прогноза собираем в один общий критерий
Этот пост является логическим продолжением предыдущего поста про два критерия оценки прогноза Форекс.
Итак, у нас есть два разных критерия, по которым мы можем сравнивать, какой из двух прогнозов оказался ближе к реальности: расстояние между графиками и коэффициент корреляции. Для удобства будем использовать не коэффициент корреляции, а корреляционное расстояние, которое выражается через коэффициент корреляции как
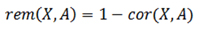
Здесь, как и в предыдущем посте, вектор A=(a1, a2, ..., aN), это реальные значения цен, вектор X=(x1, x2, ..., xN), это цены прогноза, N - число шагов прогноза.
Удобство состоит в том, что корреляционное расстояние равно нулю, когда прогноз и реальное поведение цены полностью коррелируют. Корреляционное расстояние равно единице, когда коэффициент корреляции становится равным нулю. Прогнозы с нулевым и отрицательным коэффициентами корреляции нас не интересуют, как полностью ошибочные прогнозы. Соответственно, нас не интересуют прогнозы с корреляционным расстоянием равным единице и больше единицы.
Расстояния от первого прогноза X1 на рис.3 до реального поведения цены A имеют значения
- dist(X1,A)=0.60
- rem(X1,A)=0.059
Расстояния от второго прогноза X2 на рис.3 до реального поведения цены A имеют значения
- dist(X2,A)=0.40
- rem(X2,A)=0.415
На рис.4 показано расположение этих прогнозов с рис.3 в двумерном пространстве расстояний. По горизонтальной оси отложено корреляционное расстояние, а по вертикальной оси отложено расстояние между графиками.
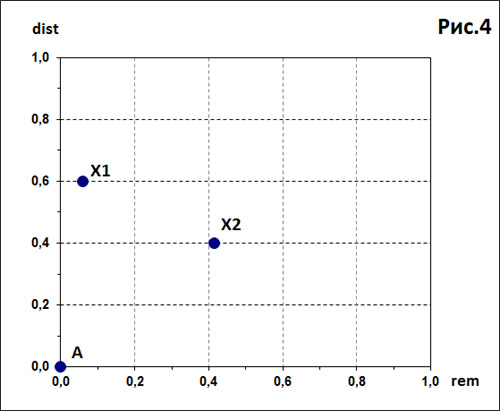
Какой же из этих двух прогнозов ближе к реальному прогнозу A, который в пространстве расстояний имеет координаты (0,0)?
Глядя на график, это сказать трудно, так как нам неизвестно, каково соотношение между корреляционным расстоянием и расстоянием между графиками.
В самом деле, если этот график на рис.4 очень сильно сжать по вертикальной оси, то получится, что от точки A до точки X1 расстояние меньше, чем от A до точки X2. И, наоборот, если график очень сильно вытянуть вдоль вертикальной оси, то получится, что от точки A до точки X1 расстояние будет больше, чем от A до точки X2.
Значит, нужно как-то нормировать эти расстояния.
Но корреляционное расстояние уже нормировано, так как коэффициент корреляции может принимать значения только от -1 до +1. Поэтому корреляционное расстояние может принимать значения только от 0 до +2. Причем расстояния от +1 до +2 нас не интересуют, так как это область бракованного прогноза, который не коррелирует с реальным поведением цен.
Хотелось бы так отнормировать расстояние между графиками, чтобы актуальными были бы тоже значения расстояний от 0 до +1. А всё, что равно +1 и выше было бы по сути бракованным прогнозом, на который не следует ориентироваться.
Автору этого поста такой естественной нормировкой представляется волатильность.
Если график прогноза находится в пределах волатильности реального поведения цен, то этот прогноз еще можно употреблять. Если график прогноза отстоит от реального поведения цен более, чем на среднюю волатильность, то это бракованный прогноз.
Саму волатильность будем определять, как среднее расстояние графиков максимумов и минимумов до графика цен закрытия.
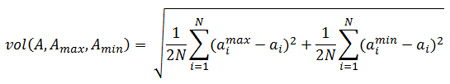
Здесь вектор A=(a1, a2, ..., aN), это реальные значения цен закрытия выбранных тайм-фреймов, а вектора Amax=(a1max, a2max, ..., aNmax) и Amin=(a1min, a2min, ..., aNmin), это, соответственно, вектора максимальных и минимальных цен на тех же тайм-фреймах.
Если расстояния между графиком прогноза и графиком реальных цен закрытия нормировать на эту волатильность, то значения нового нормированного расстояния более единицы будет означать, что график прогноза в среднем лежит за пределами волатильности. Это означает, что пользоваться таким прогнозом довольно опасно, так как стоп-лосы и тейк-профиты обычно ставятся с учетом волатильности. Следовательно, резко вырастает вероятность срабатывания стоп-лосов, а тейк-профиты срабатывать, вообще, не будут.
Итак, нормированное на волатильность расстояние между графиками будет следующим.
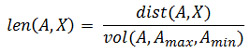
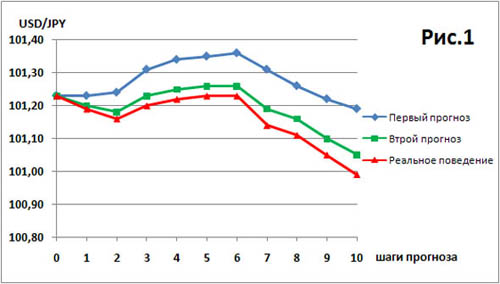
Теперь осталось сделать последний логический шаг. Надо от двумерного пространства расстояний перейти к одномерному, определив понятие расстояние на плоскости. Из курса школьной геометрии это расстояние, выраженное через координаты точки, хорошо известно.
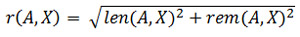
Если это обобщенное расстояние больше единице, то мы имеем дело с бракованным прогнозом. Для нормальных прогнозов обобщенное расстояние прогноза до реального поведения должно быть меньше единицы. Чем лучше прогноз, тем его расстояние до реального поведения ближе к нулю.
Рис.3 является искусственным демонстрационным учебным примером. Там неизвестны максимальные и минимальные значения цен на тайм-фреймах. Поэтому посмотрим реальные прогнозы на рис.1 и рис.2 из предыдущего поста.
На рис.5 показан свечной график реального поведения цены и два прогноза, те же самые как на рис.1.
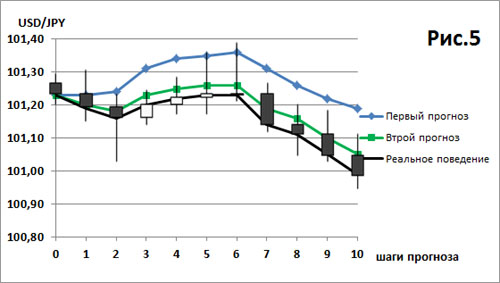
На рис.6 показан тот же самый свечной график реального поведения цены и два прогноза, те же самые как на рис.2.
Числовые значения этих свечей следующие.
| Номер шага | Цена | |||
| Открытие | Максимум | Минимум | Закрытие | |
| 0 | 101.26 | 101.29 | 101.20 | 101.23 |
| 1 | 101.23 | 101.30 | 101.15 | 101.19 |
| 2 | 101.19 | 101.23 | 101.03 | 101.16 |
| 3 | 101.16 | 101.24 | 101.14 | 101.20 |
| 4 | 101.20 | 101.28 | 101/17 | 101.22 |
| 5 | 101.22 | 101.35 | 101.17 | 101.23 |
| 6 | 101.23 | 101.38 | 101.21 | 101.23 |
| 7 | 101.23 | 101.26 | 101.12 | 101.14 |
| 8 | 101.14 | 101.20 | 101.05 | 101.11 |
| 9 | 101.11 | 101.18 | 101.03 | 101.05 |
| 10 | 101.05 | 101.11 | 100.95 | 100.99 |
Теперь можно посчитать обобщенные расстояния от прогнозов до реального поведения. (Числовые значения прогнозов на рис.5 и 6 см. в предыдущем посте.)
Для рис.5 имеем:
- r(X1,A)=1.5987
- r(X2,A)=0.4541
Таким образом, первый прогноз на рис.5 бракованный, а второй вполне приемлемый.
Если вспомнить результаты предыдущего поста, для обычного расстояния между графиками имеем
- dist(X1,A)=0.0390
- dist(X2,A)=0.0136
- rem(X1,A)=0.180
- rem(X2,A)=0.011
Если смотреть на эти расстояния, то, на первый взгляд, кажется, что для первого прогноза основной вклад в расстояние дает корреляционное расстояние, а расстояние между графиками даст только небольшую поправку. И тем самым может сложиться впечатление, что первый прогноз тоже хорош, а расстояние от него до реального поведения будет меньше единицы.
Но нормировка на волатильность всё переигрывает. Эта нормировка резко увеличивает вклад простого расстояния между графиками. И именно этот вклад становится основным. А так как простое расстояние от реального поведения до первого прогноза почти в три три раза больше, чем до второго прогноза, то и обобщенное расстояние r от реальности до первого прогноза получилось примерно в три раза больше чем до второго прогноза.
Если внимательно посмотреть на рис.5, то можно заметить, что второй прогноз расположен ближе к реальному графику, чем располагаются максимумы ножек свечей. В то время, как график цен закрытия первого прогноза пересекает только небольшое количество свечей реального поведения. А это как раз и означает, что нормированное расстояние len между первым прогнозом и реальным поведением уже больше единицы.
Теперь посмотрим результаты для рис.6.
- r(X1,A)=0.7080
- r(X2,A)=0.8028
Из предыдущего поста напоминаю, что у первого прогноза был чуть лучше результат и по корреляции и по простому расстоянию между графиками. Поэтому и обобщенное расстояние у первого прогноза чуть лучше.
Оба прогноза валидны, так как расстояния r меньше единицы. Но оба прогноза хуже, чем второй прогноз на рис.5.
Итак, обобщенное расстояние r(X,A) между вектором прогноза X и вектором реального поведения A является сбалансированным количественным показателем правильности прогноза биржевых цен на несколько тайм-фреймов вперед. Этот показатель учитывает как близость прогноза к реальности, так и похожесть поведения прогноза на реальное поведение биржевых цен.
Полезные ссылки этого сайта:
- Рейтинг брокеров Форекс
- Как начать работать на Форексе без стартового капитала
- Торговые роботы
- Калькулятор волатильности
- Калькулятор ПАММ-трейдера
- Тест регулярных прогнозов рынка Форекс
- Какие валютные пары сейчас активно покупают трейдеры, а какие валютные пары они сейчас активно распродают
- Калькулятор расчета минимально необходимого количества прибыльных сделок по известному размеру плеча, доли капитала на каждую сделку, и необходимых отстроек ордеров TakeProfit и StopLoss от уровня вхождения в рынок
- Калькулятор расчета оптимальных уровней TakeProfit и StopLoss по их заданному соотношению, по известному размеру плеча, доли капитала на сделку и средней доле прибыльных сделок
------------------
Автор статьи: Евгений Миронов,
автор книг "Формула Келли для Форекса", "Продвинутый Мартингейл", "Математическое ожидание бинарных опционов", и др
Создатель Онлайнового калькулятора на базе нейросети "Прогнозирующая Машина" для прогноза будущих цен,
Создатель Онлайнового калькулятора для анализа и формирования диверсифицированного инвестиционного портфеля из активов мосбиржи.
Хомячковый рай. Уйти и потеряться:
Два критерия оценки качества прогнозов Форекса
Если прогноз цен на рынке Форекс идет всего на один шаг вперед (например, на завтрашний день), то оценить качество прогноза достаточно просто. Мы просто смотрим, совпал ли прогноз с реальностью или нет. А если нет, то насколько реальность отличается от прогноза. Сильно или нет.
Именно так и сравниваются друг с другом два разных прогноза на предмет того, какой из двух прогнозов лучше. Тот, который в среднем дает более близкие результаты к реальности, тот прогноз и считается лучшим из двух.
А как быть, когда прогнозы даются не на один шаг вперед, а на несколько шагов. Например, как оценить качество прогноза на неделю вперед, когда в прогнозе содержатся цены закрытия по всем пяти дням недели, то есть прогноз дается сразу на 5 шагов вперед.
Допустим, Вы сравниваете два разных прогноза на несколько точек вперед, когда прошло время, и уже появились реальные данные. Тогда Вы уже можете сравнить, какой из двух прогнозов оказался лучше.
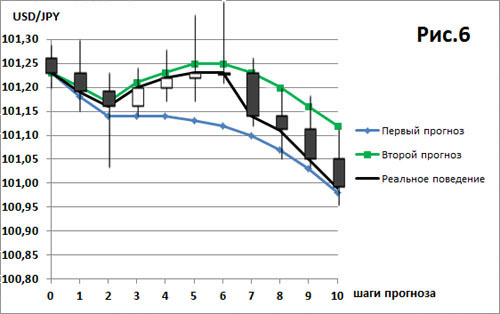
Иногда такое сравнение сделать очень легко визуальным способом. Например, на рис.1 показаны два графика прогноза цен валютной пары USD/JPY и график реального поведения цен этой валютной пары. Очень хорошо видно, что второй прогноз поведения валютной пары USD/JPY оказался гораздо точнее первого прогноза.
| Шаги прогноза | 1-й прогноз | 2-й прогноз | Реальное поведение |
| 0 | 101.23 | 101.23 | 101.23 |
| 1 | 101.23 | 101.20 | 101.19 |
| 2 | 101.24 | 101.18 | 101.16 |
| 3 | 101.31 | 101.23 | 101.20 |
| 4 | 101.34 | 101.25 | 101.22 |
| 5 | 101.35 | 101.26 | 101.23 |
| 6 | 101.36 | 101.26 | 101.23 |
| 7 | 101.31 | 101.19 | 101.14 |
| 8 | 101.26 | 101.16 | 101.11 |
| 9 | 101.22 | 101.10 | 101.05 |
| 10 | 101.19 | 101.05 | 100.99 |
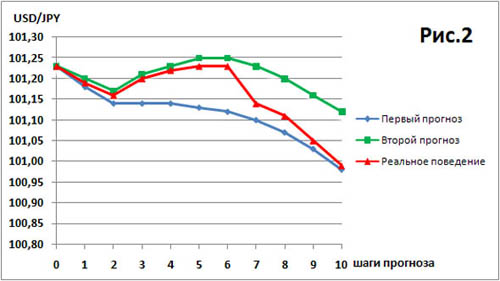
Но так красиво бывает не всегда. Понятно, что на одних шагах вперед может оказаться лучше один прогноз, а на других шагах другой прогноз. Например, на рис.2 показаны два других прогноза на том же интервале. Хорошо видно, что на отдельных шагах лучшие результаты давал один прогноз, а на других шагах лучше результаты были у другого прогноза.
| Шаги прогноза | 1-й прогноз | 2-й прогноз | Реальное поведение | 0 | 101.23 | 101.23 | 101.23 |
| 1 | 101.18 | 101.20 | 101.19 |
| 2 | 101.14 | 101.17 | 101.16 |
| 3 | 101.14 | 101.21 | 101.20 |
| 4 | 101.14 | 101.23 | 101.22 |
| 5 | 101.13 | 101.25 | 101.23 |
| 6 | 101.12 | 101.25 | 101.23 |
| 7 | 101.10 | 101.23 | 101.14 |
| 8 | 101.07 | 101.20 | 101.11 |
| 9 | 101.03 | 101.16 | 101.05 |
| 10 | 100.98 | 101.12 | 100.99 |
Чисто визуально тут очень трудно определить, какой из этих двух прогнозов является лучшим в среднем по всем 10 шагам графика.
Для оценки того, какой прогноз лучше используют понятие расстояния от графика прогноза до графика реального поведения цены валютной пары. Формула этого расстояния имеет вид:
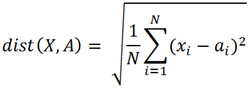
Здесь вектор A=(a1, a2, ..., aN), это реальные значения цен, вектор X=(x1, x2, ..., xN), это цены прогноза, N - число шагов прогноза.
Чисто визуально, кажется, что на рис.1 первый прогноз отстоит от реальных данных в 3-4 раза дальше, чем второй прогноз. И, действительно, вычисляя расстояния между вектором реальных цен A и векторами цен прогноза X1 и X2, мы получаем, что на рис.1 график первого прогноза расположен дальше графика второго прогноза примерно в 3.5 раза:
- dist(X1,A)=0.0390
- dist(X2,A)=0.0136
Аналогично для рис.2, вычисляя расстояния между вектором реальных цен и векторами цен двух прогнозов X1 и X2, получаем:
- dist(X1,A)=0.0602
- dist(X2,A)=0.0681
Отсюда видно, что на рис.2 в среднем первый прогноз чуточку лучше второго, так как его расстояние до графика реальных цен оказалось чуть меньше, чем расстояние от графика второго прогноза до графика реальных цен. График первого прогноза в среднем расположен более близко к графику реальных цен.
Таким образом, в качестве расстояния между графиком прогноза и графиком реального поведения, мы имеем достаточно хороший количественный критерий оценки качества прогноза поведения валютных пар (или каких-то других биржевых инструментов). Этот количественный критерий позволяет нам сравнивать между собой разные прогнозы от разных прогнозистов и делать вывод, какой из этих прогнозистов дает более качественный прогноз рыночного поведения.
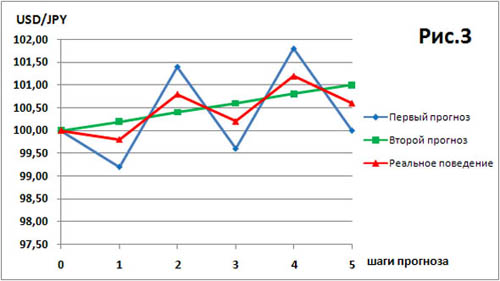
Но не всё так просто, как кажется на первый взгляд. Давай посмотрим на следующий рис.3. Это чисто учебная картинка, где намерено показано, что второй прогноз имеет меньше расстояние до реального поведения цен, чем первый прогноз. Но при этом второй прогноз ведет себя совсем не так, как реальное поведение цен.
| Шаги прогноза | 1-й прогноз | 2-й прогноз | Реальное поведение | 0 | 100.00 | 100.00 | 100.00 |
| 1 | 99.20 | 100.20 | 99.80 |
| 2 | 101.40 | 100.40 | 100.80 |
| 3 | 99.60 | 100.60 | 100.20 |
| 4 | 101.80 | 100.80 | 101.20 |
| 5 | 100.00 | 101.00 | 100.60 |
Реально цена валютной пары не только возрастала, но и совершала колебания в некотором валютном коридоре. В то время, как второй прогноз на рис.3 показывает нам только монотонный рост цен. А вот первый прогноз как раз и показывает нам сочетание роста и колебаний цен.
По критерию расстояний получается, что второй прогноз лучше первого, он ближе к реальности:
- dist(X1,A)=0.60
- dist(X2,A)=0.40
Но, что на самом деле произойдет в реальности, если мы будем следовать второму прогнозу?
Допустим, это прогноз цен закрытия на неделю вперед с понедельника по пятницу. Тогда, купив пару USD/JPY в понедельник в начале форекс-дня, мы в конце форекс-дня увидим, что прогноз и реальность существенно разошлись между собой. Валютная пара вместо роста упала в цене. А если мы поставили StopLoss на уровень 99.80, то наша открытая позиция на покупку пары USD/JPY, вообще, будет в понедельник закрыта с убытком.
В то же время, если бы мы следовали первому прогнозу, то в понедельник у нас всё было бы хорошо. Мы бы в начале форекс-дня в понедельник не купили бы, а, наоборот, продали бы пару USD/JPY. Зная, что во вторник, в соответствии с первым прогнозом, будет разворот, мы бы успели купить эту открытую позицию на продажу в понедельник в конце форекс-дня или во вторник в начале форекс-дня.
И так далее, следуя первому прогнозу, мы бы могли все 5 дней на неделе зарабатывать, несмотря на то, что первый прогноз гораздо хуже второго прогноза с точки зрения расстояния до прогноза. А вот следуя второму прогнозу, мы бы в понедельник, в среду и в пятницу сильно рисковали бы из-за того, что прогнозируемые тренды в эти дни расходятся с реальными трендами по направлению.
Это приводит нас к тому, что одного только критерия оценки прогноза по расстоянию до реального графика цен уже недостаточно для качественной оценки прогноза, выдаваемого прогнозистом. Нужен еще один математический критерий, который учитывает коррелированность прогноза и реального поведения.
Таким критерием является коэффициент корреляции:
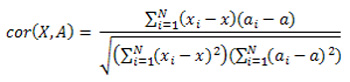
Здесь x и a, это средние значения наборов чисел X=(x1, x2, ..., xN) и A=(a1, a2, ..., aN), соответственно, то есть
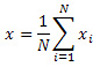 ,
, 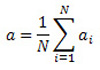
Коэффициент корреляции находится в пределах от -1 до +1. Если график прогноза в точности повторяет все изменения реального ценового графика (независимо от расстояния до него), то коэффициент корреляции прогноза и реального поведения будет равен +1. Если график прогноза в точности повторяет все изменения реального ценового графика с точностью до наоборот (как отражение в зеркале, вместо роста падение, а вместо падения рост), то коэффициент корреляции прогноза и реального поведения будет равен -1. Если прогноз и реальное поведение никак не коррелируют между собой, то коэффициент корреляции равен нулю.
Теперь посчитаем коэффициенты корреляции прогнозов с поведением цены на рис.3:
- cor(X1,A)=0.941
- cor(X2,A)=0.585
Получается, что первый прогноз очень хорошо коррелирует с поведение цены. Его коэффициент корреляции достаточно близок к +1. Второй прогноз тоже неплохо коррелирует с поведением цены, коэффициент корреляции больше чем +0.5. У них же совпадают тренды за все 5 дней. Но коэффициент корреляции второго прогноза с поведением цены значительно уступает коэффициенту корреляции первого прогноза с поведением цены, так как второй прогноз очень грубый, он не показывает более "тонкую" структуру основного тренда.
Посмотрим для интереса коэффициенты корреляции прогнозов с реальным поведением цен на рис.1 и рис.2.
Для рис.1 имеем:
- cor(X1,A)=0.820
- cor(X2,A)=0.989
Коэффициент корреляции второго прогноза очень близок к +1, так как второй прогноз на рис.1 точно повторяет все тенденции реального поведения цены. Первый прогноз тоже неплохо коррелирует с реальностью, но на шагах 1 и 2 этот прогноз прогнозирует тенденцию к повышению цены, а не к понижению. Это факт занижает коэффициент корреляции первого прогноза с реальностью на рис.1.
Для рис.2 имеем:
- cor(X1,A)=0.905
- cor(X2,A)=0.876
Оба прогноза на рис.2 неплохо коррелируют с реальным поведением цены. Но хуже, чем второй прогноз на рис.1 и лучше, чем первый прогноз на рис.1.
Обратите внимание, что на рис.2 первый прогноз оказался лучше второго не только по расстоянию до реальности, но и по корреляции с реальностью. И это не смотря на то, что с 3-го по 6-й шаги первый прогноз неправильно прогнозирует направление тренда. Эта ошибка первого прогноза компенсируется очень сильными корреляциями с реальностью на других шагах прогнозирования. Особенно на шагах 7-10.
Итак, мы имеем два основных критерия для оценки качества прогнозов валютных курсов: расстояние от прогноза до реального поведения цен и коэффициент корреляции прогноза и реального поведения цен.
Если Вам предлагают воспользоваться несколькими биржевыми прогнозами, но при этом эти прогнозы прогнозируют совершенно разные направления трендов и/или разные типы поведения цены, то необходимо провести сравнение этих прогнозов на исторических данных на соответствие обеим критериям. После чего можно будет сделать уже осмысленный выбор и отдать предпочтение тем прогнозам, у которых наилучшие показатели корреляции и расстояний с реальным поведением цен.
Наконец, с помощью этих двух критериев можно просто отбраковывать все некачественные прогнозы. К некачественным прогнозам относятся такие прогнозы, коэффициент корреляции которых с реальным поведением цены близок к нулю или отрицательный. А также некачественным прогнозом является такой прогноз, у которого расстояние до реального поведения цены превышает волатильность поведения данной валютной пары.
Полезные ссылки этого сайта:
- Рейтинг брокеров Форекс
- Как начать работать на Форексе без стартового капитала
- Торговые роботы
- Калькулятор волатильности
- Калькулятор ПАММ-трейдера
- Тест регулярных прогнозов рынка Форекс
- Какие валютные пары сейчас активно покупают трейдеры, а какие валютные пары они сейчас активно распродают
- Калькулятор расчета минимально необходимого количества прибыльных сделок по известному размеру плеча, доли капитала на каждую сделку, и необходимых отстроек ордеров TakeProfit и StopLoss от уровня вхождения в рынок
- Калькулятор расчета оптимальных уровней TakeProfit и StopLoss по их заданному соотношению, по известному размеру плеча, доли капитала на сделку и средней доле прибыльных сделок
------------------
Автор статьи: Евгений Миронов,
автор книг "Формула Келли для Форекса", "Продвинутый Мартингейл", "Математическое ожидание бинарных опционов", и др
Создатель Онлайнового калькулятора на базе нейросети "Прогнозирующая Машина" для прогноза будущих цен,
Создатель Онлайнового калькулятора для анализа и формирования диверсифицированного инвестиционного портфеля из активов мосбиржи.




