Влияние минимальной прибыли на стратегию Мартингейла. Часть3
(Окончание. Предыдущую статью см. здесь.)
Недостаток уменьшения минимальной прибыли
Итак, чем больше заданная минимальная прибыль, тем быстрее нарастают убытки в серии убыточных сделок. А чем меньше заданная минимальная прибыль, тем нарастание убытков идет медленнее.
Казалось бы, вот это и есть решение проблемы слишком быстрого нарастания убытков в серии убыточных сделок. Но тут опять не всё так просто.
Если сравнить последние колонки таблиц 7 и 9, и, особенно, таблиц 8 и 10, то видно, что, чем меньше минимальная прибыль, тем меньше нарастает капитал игрока при одной и той же вероятности прибыльных сделок.
Пусть, как и раньше, вероятность прибыльных сделок будет p=0.6. Тогда в среднем на каждую сделку капитал увеличивается со скоростями, представленными в таблице 11. (В расчетах бралось распределение убыточных серий для серии из 100 сделок.)
Таблица 11.
| Округление/мин.прибыль | R=0.5 | R=0.8 | R=1 |
| До целого | 0.45 | 0.62 | 0.9 |
| До 0.1 | 0.33 | 0.49 | 0.62 |
| До 0.01 | 0.3 | 0.48 | 0.6 |
| Без округления | 0.3 | 0.48 | 0.6 |
Эта таблица показывает среднюю скорость роста капитала относительно базовой ставки. Во всех этих случаях базовая ставка равна единице.
Как можно корректно сравнить между собой поведение капитала игрока для разных значений минимальной прибыли?
Есть два способа такого сравнения.
В первом способе будем считать, что у нас одно и то же соотношение стартового капитала и базовой ставки. Допустим, базовая ставка равна 1% от стартового капитала.
Тогда в Проксима для количества процентов от стартового капитала в стартовой ставке вводим 2% для минимальной прибыли 1 и округления до целого, и 1% для минимальных прибылей 0.8 и 0.5 и округления до целого.
На рисунках 8 показано, как в этих случаях может меняться стартовый капитал на серии 100 сделок.
Если условие прекращения стратегии не наступает, то больше всего зарабатывают те игроки, которые в качестве минимальной прибыли используют 1 и, соответственно, стартовую ставку, равную 2% от стартового капитала. В среднем, за 100 сделок, они увеличивают свой капитал на 90% (рис.8а).
А хуже всего обстоят дела у игроков, которые в качестве минимальной прибыли используют 0.5 и, соответственно, стартовую ставку 1% от стартового депозита. В случае везения, они за 100 сделок увеличивают свой стартовый капитал, в среднем, только на 45% (рис.8в).
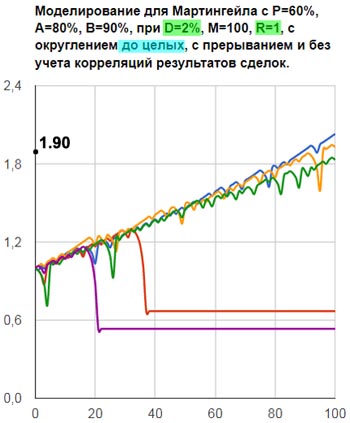
Рис.8а
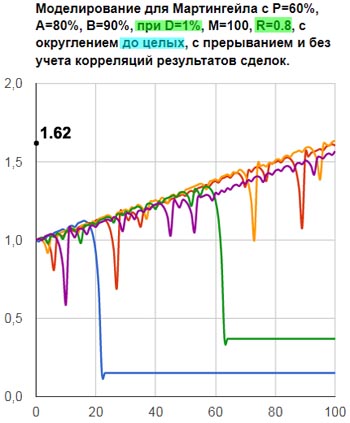
Рис.8б
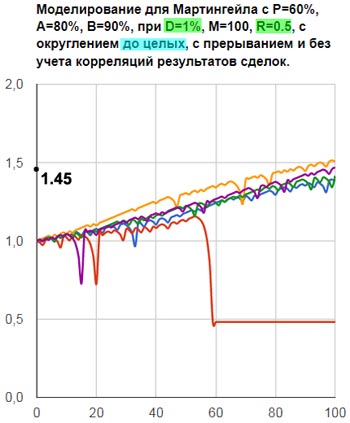
Рис.8в
Аналогично, при отсутствии округления в Проксима вводим 1.25% для минимальной прибыли 1, вводим 1% для минимальной прибыли 0.8, и вводим 0.625% для минимальной прибыли 0.5. На рисунках 9 смотрим результат.
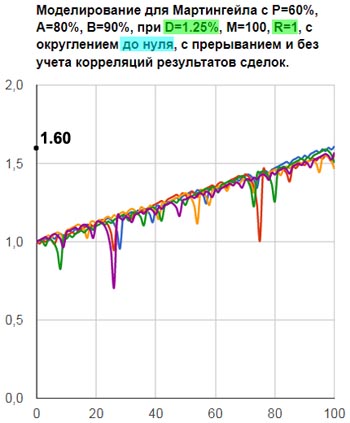
Рис.9а
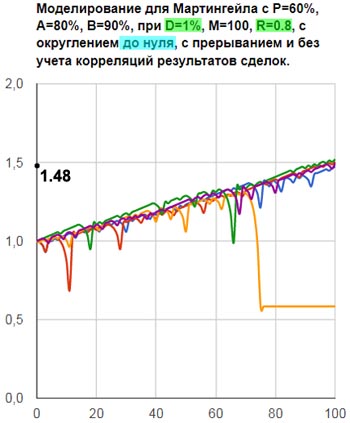
Рис.9б
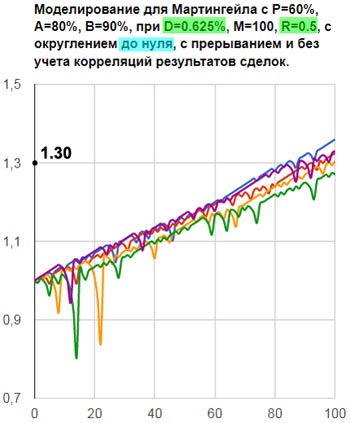
Рис.9в
И тут для минимальной прибыли 0.5 получается за 100 сделок рост стартового капитала в 2 раза меньше, чем для минимальной прибыли, равной 1.
Шесть предыдущих графиков надо понимать следующим образом.
Например, в таблице 11 показано, что без округления чисел Мартингейла для заданной минимальной прибыли 0.5, средняя скорость роста капитала будет 0.3 в единицах базовой ставки. Значит, на 100 сделок, в среднем, ожидаем увеличение капитала на 0.3*100=30 базовых ставок. Но у нас базовая ставка равна 1% стартового капитала. (Поэтому стартовая ставка равна 0.625% от стартового капитала.) Значит, 30 базовых ставок, это 30% стартового капитала. Вот и получается на рис.9в, что за 100 сделок стартовый капитал увеличился в 1.3 раза.
Но не всегда бывает удобно оперировать базовыми ставками. В наших примерах мы просто заранее знаем, во сколько раз отличаются друг от друга базовая ставка и стартовые ставки для разных параметров. А на практике часто бывает другая ситуация. Это ситуация, когда игрок заранее знает, какую долю своего капитала он хочет использовать в качестве стартового капитала.
Для этого в Проксима предусмотрен ввод процентного соотношения стартовой ставки к стартовому капиталу.
Кроме того, если стартовая ставка не совпадает с базовой ставкой, то в качестве результатов выводится еще таблица Мартингейла, нормированная на стартовую ставку. В ней все числа Мартингейла разделены на стартовую ставку. Поэтому стартовая ставка в такой таблице Мартингейла всегда равна единице.
Это бывает более удобно для практического применения.
Поэтому теперь посмотрим, как будет увеличиваться один и тот же стартовый капитал, если в нем применяется одна и та же стартовая ставка. Но с разными округлениями и минимальной прибылью.
Для этого просто берем данные таблицы 11 и делим их на соответствующие им стартовые ставки. Получаем таблицу 12, которая показывает средние скорости роста капитала, нормированные на стартовую ставку.
Таблица 12.
| Округление/мин.прибыль | R=0.5 | R=0.8 | R=1 |
| До целого | 0.45 | 0.62 | 0.45 |
| До 0.1 | 0.47 | 0.49 | 0.48 |
| До 0.01 | 0.48 | 0.48 | 0.48 |
| Без округления | 0.48 | 0.48 | 0.48 |
В этой таблице колонки для R=0.5 и R=1 получились совершенно одинаковыми. Так оно и должно быть.
Например, если сравнить таблицу 7 и таблицу 9, то можно увидеть, что в таблице 7 стоят удвоенные числа из таблицы 9. Причём, в таблице 7 стартовая ставка равна 2, а в таблице 9 стартовая ставка равна 1. Поэтому, когда нормируем эти таблицы на их стартовые ставки, то получаем две совершенно одинаковые таблицы чисел Мартингейла.
Поэтому, если теперь мы хотим в Проксима считать, что отношение стартового капитала и стартовой ставки одинаковое во всех трех случаях и стартовая ставка составляет, например, 1% от стартового капитала, то видно, что на серии 100 сделок и при R=0.5 и при R=1 стартовый капитал увеличивается примерно одинаково. Сравните рис.8а и 8в. На рис. 8а рост был в 2 раза больше только лишь потому, что там стартовая ставка была взята в 2 раза больше, чем на рис.8в. А так, это два совершенно одинаковых Мартингейлов.
P.S.
По материалам книги "Продвинутый Мартингейл".
Проксима - это продвинутый калькулятор и симулятор стратегий Мартингейла для фондовой биржи, Форекса, бинарных опционов и азартных игр.
------------------
Автор статьи: Евгений Миронов,
автор книг "Формула Келли для Форекса", "Продвинутый Мартингейл", "Математическое ожидание бинарных опционов", и др
Создатель Онлайнового калькулятора на базе нейросети "Прогнозирующая Машина" для прогноза будущих цен,
Создатель Онлайнового калькулятора для анализа и формирования диверсифицированного инвестиционного портфеля из активов мосбиржи.


