Формула идеального Мартингейла
(Продолжаем серию статей, посвященных стратегии Мартингейла.)
Здесь рассмотрим еще один материал из книги "Продвинутый Мартингейл". Этот материал посвящен формуле идеального Мартингейла. Эта формула практически никогда не встречается, так как капитал не является бесконечно делимым, а ставки не могут быть дробями с бесконечным числом знаков после запятой.
Но есть один случай в рулетке и один случай в бинарных опционах, когда формула идеального Мартингейла работает. И, кроме того, как вы уже хорошо знаете, на Форексе и на фондовой или крипто бирже вы всегда можете выбирать тот вид Мартингейла, который вам больше нравится.
Формула для ставок идеального Мартингейла, нормированных на базовую ставку имеет вид:
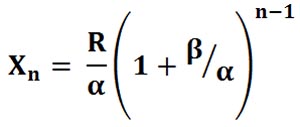
где n, это номер сделки в серии убыточных сделок. (Все обозначения здесь, как в книге (или см. предыдущие статьи).)
Формула для накопленного убытка в идеальном Мартингейле при нормировке на базовую ставку имеет вид:
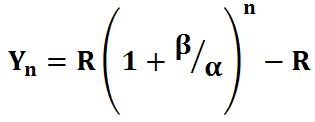
где n, это тоже номер сделки в серии убыточных сделок.
Некоторые люди удивляются, как такие формулы могут быть формулами идеального Мартингейла, если они тоже дают дробные последовательности Мартингейла. Им кажется, что дробные числа Мартингейла не решают проблему быстрого наращивания убытков в серии убыточных сделок.
Но в определении идеального Мартингейла нигде не говорится, что последовательность идеального Мартингейла должна состоять только из целых чисел. (Это фантазии тех, кто плохо читал теорию Мартингейла.) Если у вас какое-то недопонимание этих вещей, то, прежде чем читать дальше, советую еще раз прочитать, что называется идеальным Мартингейлом.
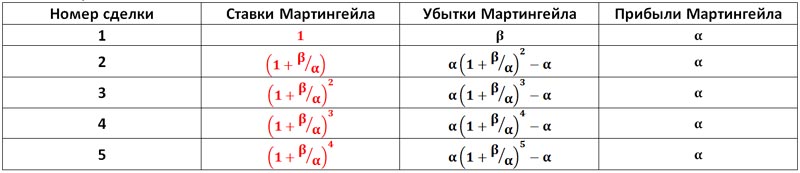
Таблица идеального Мартингейла выглядит так.
Таблица 13.
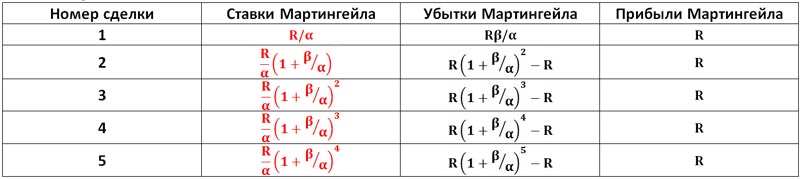
Теперь понятно, откуда в нашем примере взялось “волшебное” число 2.125, которое является отношением ставки Мартингейла к предыдущей ставке. Это число (1+β/α)=2.125 при α=0.8 и β=0.9.
Прибыли Мартингейла получаются всегда одинаковыми и равными минимальной прибыли, так как
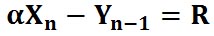
При α=R стартовая ставка равна базовой ставке Мартингейла. Формулы для ставок и для убытков становятся, соответственно, такими:
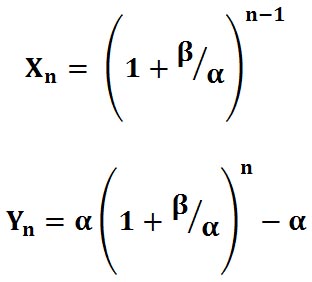
А верхняя часть таблицы Мартингейла для этого случая выглядит так.
Таблица 14.
Теперь понятно, когда идеальный Мартингейл встречается на практике. На практике идеальный Мартингейл встречается, когда являются целыми числами, одновременно, и отношение R/α и (1+β/α).
Таблица 15 дает представление о том, при каких параметрах R, α и β идеальный Мартингейл получается на практике.
Таблица 15.

Колонка этой таблицы для (1+β/α)=2 соответствует самой известной стратегии Мартингейла, когда потери в убыточной сделке равны выигрышу в прибыльной сделке. То есть когда α=β. И при этом минимальная прибыль должна быть кратна α. То есть минимальная прибыль задается кратной базовой прибыли.
Например, при игре в европейскую рулетку при ставках на чёрное и красное игрок или теряет всю ставку (β=1), или зарабатывает столько же, сколько поставил (α=1). Значит, если в качестве минимальной прибыли игрок выбирает целое число базовых прибылей, то получается идеальный Мартингейл. В этом случае пропорциональное увеличение стартового капитала и стартовой ставки с целью использовать дробные значения стартовой ставки не приводит к нужному эффекту. Но и не вредит.
Случай R=α=β интересен тем, что в этом случае стартовая ставка совпадает и с базовой ставкой и с базовой прибылью. Таблица 16 с удвоением ставок всем хорошо известна.
Таблица 16.
| Номер сделки | Ставки Мартингейла | Убытки Мартингейла | Прибыли Мартингейла |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 3 | 1 |
| 3 | 4 | 7 | 1 |
| 4 | 8 | 15 | 1 |
| 5 | 16 | 31 | 1 |
| 6 | 32 | 63 | 1 |
| 7 | 64 | 127 | 1 |
Другие случаи для (1+β/α)=2 особого интереса не представляют. Это просто увеличение стартовой ставки в целое число раз. Например, таблица Мартингейла для случая 2R=α=β показана в таблице 17.
Таблица 17.
| Номер сделки | Ставки Мартингейла | Убытки Мартингейла | Прибыли Мартингейла |
| 1 | 2 | 2 | 2 |
| 2 | 4 | 6 | 2 |
| 3 | 8 | 14 | 2 |
| 4 | 16 | 30 | 2 |
| 5 | 32 | 62 | 2 |
| 6 | 64 | 126 | 2 |
| 7 | 128 | 254 | 2 |
Таблица 17 содержит просто удвоенные значения чисел Мартингейла из таблицы 16. И не более. Если при этом ещё и удвоить стартовый капитал, то стратегия Мартингейла в таблице 17 не будет иметь никаких недостатков или преимуществ по сравнению со стратегией Мартингейла из таблицы 16.
На бинарных опционах использовать идеальный Мартингейл с (1+β/α)=2 не получится, так как на бинарных опционах всегда α<β.
А вот в биржевой торговле идеальный Мартингейл с (1+β/α)=2 вполне применим. При этом ордера TakeProfit и StopLoss надо устанавливать всегда так, чтобы с учетом всех комиссий всегда было α=β. И нужно всегда устанавливать ордера TakeProfit и StopLoss так, чтобы значения α и β в каждой сделке оставались постоянными.
Например, если решено, что α=β=0.05, то, в каждой сделке надо пересчитывать значения цен TakeProfit и StopLoss так, чтобы всегда было α=β=0.05. То есть при срабатывании ордера TakeProfit, капитал, участвующий в сделке должен всегда увеличиваться на 5%. А при срабатывании ордера StopLoss, капитал, участвующий в сделке должен всегда уменьшаться на 5%.
Для (1+β/α)=3 убытки на убыточной сделке должны быть в 2 раза больше, чем прибыль на прибыльной сделке.
Это, например, могут быть бинарные опционы с потерей всей ставки на убыточной сделке (β=100%) и выплатой половины ставки на прибыльной сделке (α=50%). Или это может быть бинарный опцион с частичным возвратом ставки в убыточной сделке. Например, α=40%, β=80%; или α=30%, β=60%; и т.д., главное, чтобы α было всегда в 2 раза меньше, чем β.
В таблице 18 даны, для примера, числа Мартингейла для 2R=2α=β, когда β=1, α=0.5 и R=0.5. При любом округлении получается одна и та же таблица чисел Мартингейла, которая соответствует идеальной стратегии Мартингейла.
Таблица 18.
| Номер сделки | Ставки Мартингейла | Убытки Мартингейла | Прибыли Мартингейла |
| 1 | 1 | 1 | 0.5 |
| 2 | 3 | 4 | 0.5 |
| 3 | 9 | 13 | 0.5 |
| 4 | 27 | 40 | 0.5 |
| 5 | 81 | 121 | 0.5 |
| 6 | 243 | 364 | 0.5 |
| 7 | 729 | 1093 | 0.5 |
Вместо удвоения ставок здесь идет утроение ставок.
При биржевой торговле условие (1+β/α)=3 соответствует такой расстановке ордеров TakeProfit и StopLoss, при которой в случае убыточной сделки теряется в 2 раза больше, чем зарабатывается в прибыльной сделке. В отличие от бинарных опционов, биржевая торговля позволяет трейдеру самому принимать решение, какими будут значения α и β на протяжении всей игры.
Наконец, посмотрим на формулы идеального Мартингейла, нормированные на стартовую ставку, то есть, когда стартовая ставка всегда равна 1.
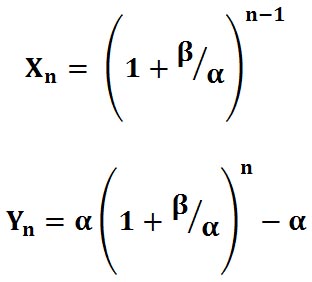
Нетрудно заметить, что эти формулы в точности совпадают с соответствующими формулами для случая, когда минимальная прибыль совпадает с базовой прибылью (α=R).
P.S.
По материалам книги "Продвинутый Мартингейл". Эта книга поможет Вам, если Вы хотите досконально разобраться во всех тонкостях Мартингейла. На сегодня, это единственный в мире источник на русском языке с полным описанием всех стратегий Мартингейла, которые можно применять и на бирже и в азартных играх.
Проксима - это продвинутый калькулятор и симулятор стратегий Мартингейла для фондовой биржи, Форекса, бинарных опционов и азартных игр. На сегодня, это единственный в мире полный калькулятор и симулятор стратегии Мартингейла на русском языке. Этот онлайновый сервис бесплатный!
------------------
Автор статьи: Евгений Миронов,
автор книг "Формула Келли для Форекса", "Продвинутый Мартингейл", "Математическое ожидание бинарных опционов", и др
Создатель Онлайнового калькулятора на базе нейросети "Прогнозирующая Машина" для прогноза будущих цен,
Создатель Онлайнового калькулятора для анализа и формирования диверсифицированного инвестиционного портфеля из активов мосбиржи.


