Рассмотрим, как на автокорреляционной функции отражается снижение возможности прогнозирования поведения линейной функции, на которую наложен равнораспределенный симметричный белый шум.
Отсутствие шума
Рассмотрение проведем на примере самой простой линейной функции y(x)=x. Возьмем выборку значений этой функции, например, в точках x=0,1,2,3,.... Будем считать, что мы не знаем, откуда взялись эти данные. Например, это могут быть результаты измерений какой-то физической величины с течением времени, или это изменение цены какого-то финансового актива с течением времени. В общем, какой-то процесс во времени.
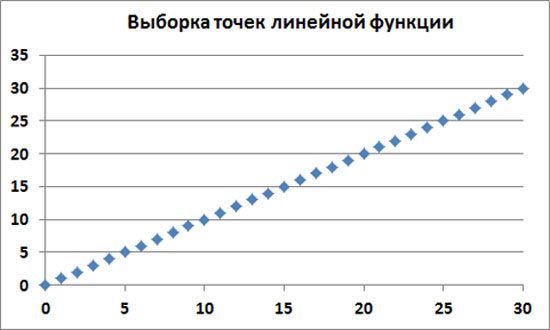
Посчитаем эмпирическую автокорреляционную функцию R(t) для данной выборки, например, для скользящего окна размером 250 точек. Разумеется, мы получим эмпирическую автокорреляционную функцию точно такую же, как и теоретическую автокорреляционную функцию для бесконечно длинной непрерывной функции y(x)=x. То есть автокорреляционная функция везде будет равна значению единица R(t)=1.
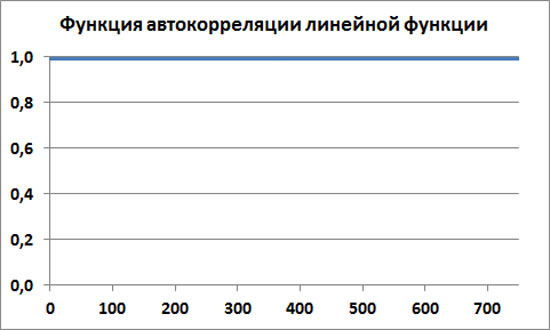
Это и понятно, ведь любые участки такого процесса всегда коррелируют друг с другом. И мы всегда можем спрогнозировать, какие будут следующие значения этого процесса, даже не зная, что за основу была взята функция y(x)=x.
Например, если это цена какого-то финансового актива, то мы просто покупаем этот актив и тупо ждем, когда цена достигнет нужного нам значения, чтобы продать этот актив. Например, так растет банковский депозит по схеме начисления простых процентов. Никаких случайностей.
Здесь и везде далее будем рассматривать процесс (временной ряд) начиная с точки x=0 и при x≥0. Поэтому и функция автокорреляции будет определяться для x≥0.
Добавление шума с амплитудой 25
Добавим в наш хорошо прогнозируемый процесс случайный шум. Пусть, для простоты, это будет стационарный равнораспределенный белый шум в интервале от -25 до +25. Сразу замечу, что если взять нестационарный шум или шум с неравномерным распределением (например, гауссовский), то, принципиально, качественная картина не изменится.
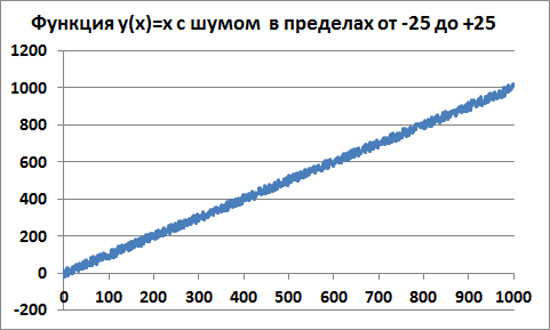
Прогнозируемость процесса уже не 100%-ная. На временных участках менее 50 прогнозируемость уже отсутствует. Например, если это биржевая цена, то, купив в момент времени x1=200, вряд ли можно предсказать, какая будет цена в момент времени x2=220. Ведь разница x2-x1=20 меньше, чем амплитуда шума 25.
Но если разница Δx=x2-x1 будет много больше 25, то будет нормальная прогнозируемость.
Другими словами, на больших тайм-фреймах все индикаторы технического анализа дружно покажут, что восходящий тренд будет продолжен. Точно также, как они показывали это на графике без шума.
А на маленьких тайм-фреймах (меньше 25) будет разнобой показаний индикаторов. Одни индикаторы покажут, что будет рост цены, другие покажут, что будет падение цены.
Посчитаем эмпирическую автокорреляционную функцию для данной выборки с шумом амплитудой 25 для скользящего окна размером 250 точек. Получается такой график.
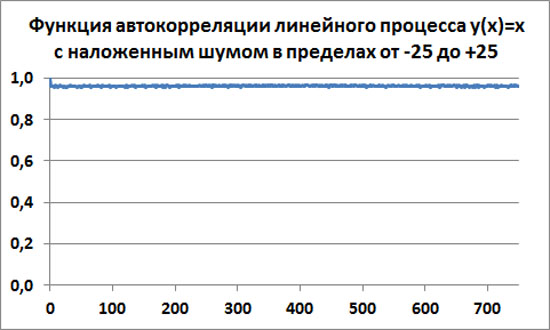
В точке x=0 функция автокорреляции всегда равна единице R(0)=1. Затем она резко падает к среднему значению Ra=0.96. Возле этого среднего значения автокорреляционная функция далее совершает случайные колебания со среднеквадратичным отклонением примерно σ=0.0026.
Добавление шума с амплитудой 100
Теперь добавим к линейной функции стационарный равнораспределенный белый шум в интервале от -100 до +100.
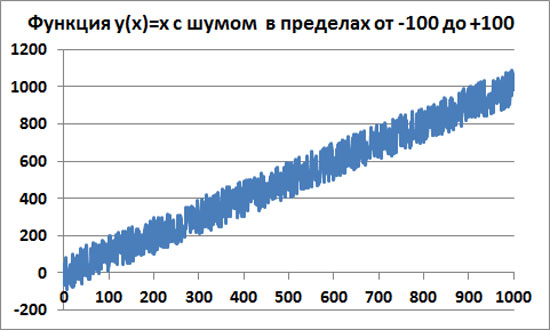
Эффект непредсказуемости поведения процесса усилился. Теперь предсказуемость процесса исчезает уже на интервалах Δx менее 100. Но на более длинных интервалах по прежнему просматривается хороший предсказуемый тренд.
Также посчитаем эмпирическую автокорреляционную функцию для данного случая для скользящего окна размером 250 точек.
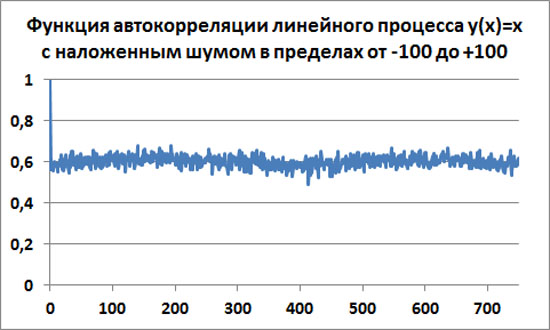
После R(0)=1, функция автокорреляции резко падает к среднему значению Ra=0.61. Возле этого среднего значения автокорреляционная функция далее совершает случайные колебания со среднеквадратичным отклонением примерно σ=0.0273.
Добавление шума с амплитудой 200
Теперь всё то же самое, но амплитуда шума в интервале от -200 до +200.
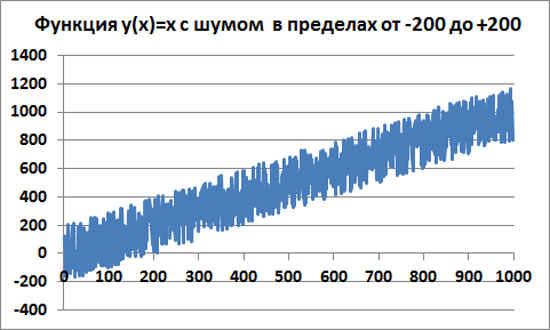
Автокорреляцию считаем тоже для скользящего окна размером 250 точек.
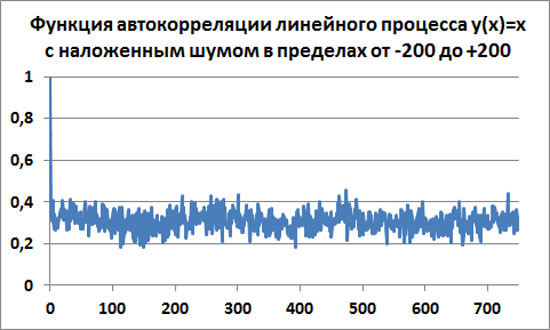
После R(0)=1, функция автокорреляции резко падает к среднему значению Ra=0.28 и далее идут случайные колебания со среднеквадратичным отклонением примерно σ=0.0487.
Добавление шума с амплитудой 500
Ещё с амплитудой шума в интервале от -500 до +500.
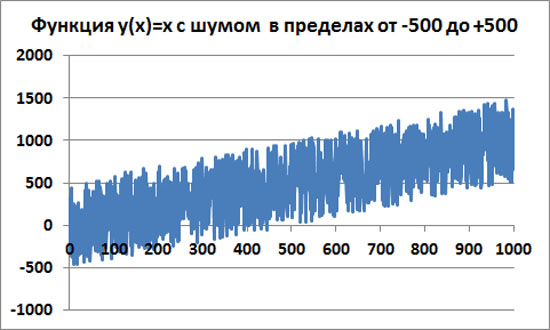
Автокорреляцию считаем также для скользящего окна размером 250 точек.
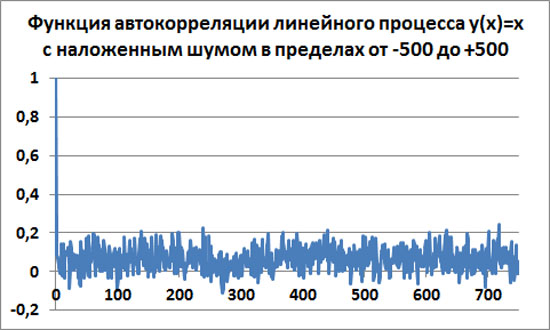
Функция автокорреляции падает с единицы к среднему значению Ra=0.06 и далее идут хаотические колебания со среднеквадратичным отклонением примерно σ=0.0609.
Добавление шума с амплитудой 2500
Наконец, добавим такой шум, чтобы тренд полностью утопить в этом шуме, чтобы тренд совсем не ощущался на интервале от x=0 до x=1000. Добавим шум с амплитудой 2500.
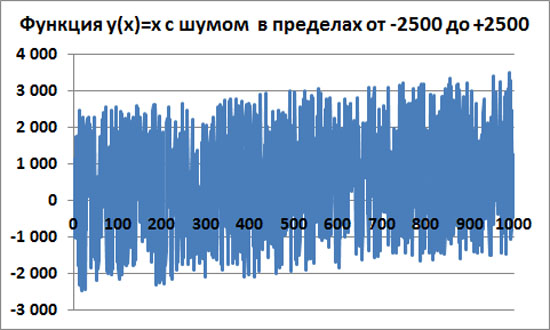
Понятно, что если этот график продолжить от x=0 до, например, x=5000, то тренд визуально проявится. То есть на очень больших тайм-фреймах индикаторы технического анализа обнаружат хороший восходящий тренд.
Но на нашем графике от x=0 до x=1000 уже не видно никакого тренда. Индикаторы технического анализа на нашем графике уже не смогут детектировать наличие восходящего тренда. Изменение параметров этих индикаторов на данном интервале приводит к сильному изменению их прогнозов.
Автокорреляцию считаем также для скользящего окна размером 250 точек.
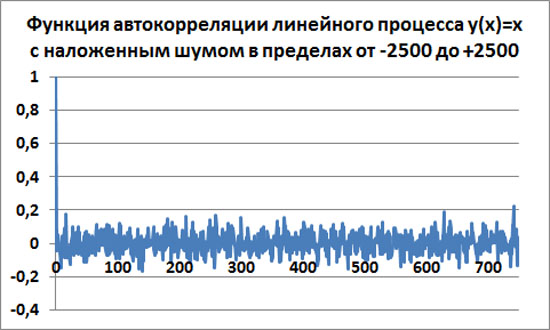
Функция автокорреляции падает с единицы практически к нулевому среднему значению Ra=0. Но среднеквадратичное отклонение немного увеличивается по равнению с предыдущим случаем и примерно равно σ=0.0633.
Только шум
Если бы у нас был бы только шум, то теоретическая функция автокорреляции для бесконечно длинного процесса была бы R(0)=1 и R(t)=0 для любого t>0.
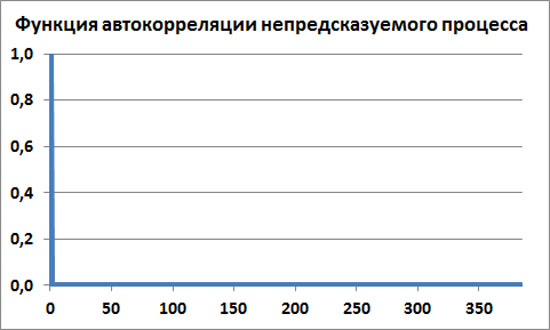
Тенденция при увеличении непредсказуемости
По мере того, как непредсказуемый шум, наложенный на регулярный предсказуемый процесс, усиливается, для t>0 функция автокорреляции R(t) стремиться к нулю.
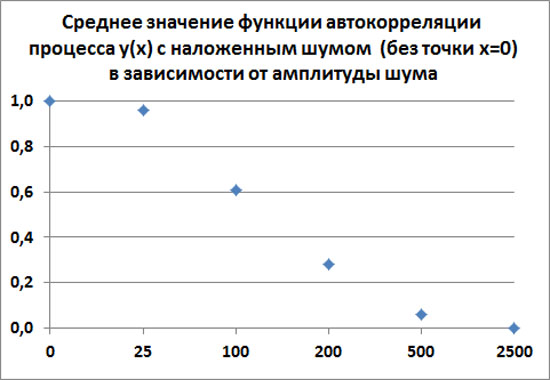
При очень большой амплитуде шума, когда регулярный тренд уже становится незаметным, функция автокорреляции при t>0 в среднем находится около нуля. Но при этом среднеквадратичное отклонение от нуля нарастает при усилении шума.
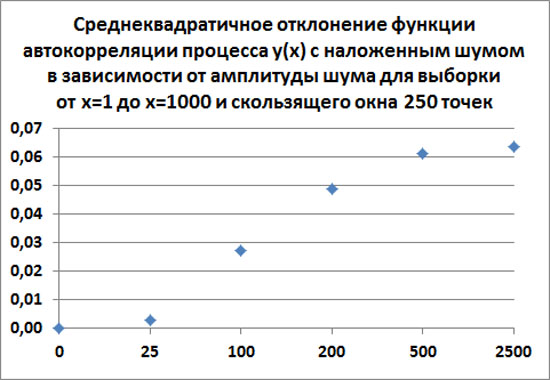
Этот эффект связан исключительно с тем, что, при вычислении эмпирической функции автокорреляции, приходится использовать выборку конечной величины. Если увеличивать размер скользящего окна и размер общего интервала, из которого берется выборка, то среднеквадратичное отклонение также будет стремиться к нулю.
Вот, например, как уменьшается среднеквадратичное отклонение автокорреляционной функции от нуля, если выборку не увеличивать, а увеличивать размер скользящего окна. Этот график показывает зависимость среднеквадратичного отклонения от размера скользящего окна, когда на регулярную линейную зависимость наложили шум с амплитудой 2500.
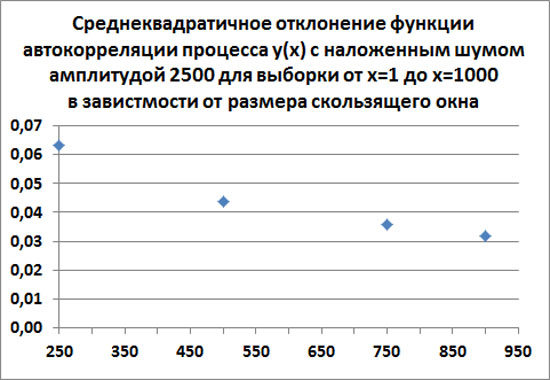
В данном случае, при стремлении размера скользящего окна к размеру всего интервала, из которого берется выборка, среднеквадратичное отклонение от нуля стремиться к некоторому конечному пределу. В данном случае примерно к σ=0.03.
Если выборку делать не по 1000 точек, а больше, то это предельное значение σ будет меньше чем 0.03. При стремлении выборки к бесконечности, это предельное значение σ будет стремиться к нулю. И график эмпирической функции автокорреляции будет стремиться к графику теоретической функции автокорреляции. То есть в пределе будет R(t)=0 для любого t>0.